vedo.pointcloud

   1#!/usr/bin/env python3
   2# -*- coding: utf-8 -*-
   3import time
   4from weakref import ref as weak_ref_to
   5
   6from typing import Union, List
   7from typing_extensions import Self
   8
   9import numpy as np
  10
  11import vedo.vtkclasses as vtki
  12
  13import vedo
  14from vedo import colors
  15from vedo import utils
  16from vedo.transformations import LinearTransform, NonLinearTransform
  17from vedo.core import PointAlgorithms
  18from vedo.visual import PointsVisual
  19
  20__docformat__ = "google"
  21
  22__doc__ = """
  23Submodule to work with point clouds.
  24
  25![](https://vedo.embl.es/images/basic/pca.png)
  26"""
  27
  28__all__ = [
  29    "Points",
  30    "Point",
  31    "merge",
  32    "fit_line",
  33    "fit_circle",
  34    "fit_plane",
  35    "fit_sphere",
  36    "pca_ellipse",
  37    "pca_ellipsoid",
  38]
  39
  40
  41####################################################
  42def merge(*meshs, flag=False) -> Union["vedo.Mesh", "vedo.Points", None]:
  43    """
  44    Build a new Mesh (or Points) formed by the fusion of the inputs.
  45
  46    Similar to Assembly, but in this case the input objects become a single entity.
  47
  48    To keep track of the original identities of the inputs you can set `flag=True`.
  49    In this case a `pointdata` array of ids is added to the output with name "OriginalMeshID".
  50
  51    Examples:
  52        - [warp1.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/warp1.py)
  53
  54            ![](https://vedo.embl.es/images/advanced/warp1.png)
  55
  56        - [value_iteration.py](https://github.com/marcomusy/vedo/tree/master/examples/simulations/value_iteration.py)
  57
  58    """
  59    objs = [a for a in utils.flatten(meshs) if a]
  60
  61    if not objs:
  62        return None
  63
  64    idarr = []
  65    polyapp = vtki.new("AppendPolyData")
  66    for i, ob in enumerate(objs):
  67        polyapp.AddInputData(ob.dataset)
  68        if flag:
  69            idarr += [i] * ob.dataset.GetNumberOfPoints()
  70    polyapp.Update()
  71    mpoly = polyapp.GetOutput()
  72
  73    if flag:
  74        varr = utils.numpy2vtk(idarr, dtype=np.uint16, name="OriginalMeshID")
  75        mpoly.GetPointData().AddArray(varr)
  76
  77    has_mesh = False
  78    for ob in objs:
  79        if isinstance(ob, vedo.Mesh):
  80            has_mesh = True
  81            break
  82
  83    if has_mesh:
  84        msh = vedo.Mesh(mpoly)
  85    else:
  86        msh = Points(mpoly) # type: ignore
  87
  88    msh.copy_properties_from(objs[0])
  89
  90    msh.pipeline = utils.OperationNode(
  91        "merge", parents=objs, comment=f"#pts {msh.dataset.GetNumberOfPoints()}"
  92    )
  93    return msh
  94
  95
  96def _rotate_points(points, n0=None, n1=(0, 0, 1)) -> Union[np.ndarray, tuple]:
  97    # Rotate a set of 3D points from direction n0 to direction n1.
  98    # Return the rotated points and the normal to the fitting plane (if n0 is None).
  99    # The pointing direction of the normal in this case is arbitrary.
 100    points = np.asarray(points)
 101
 102    if points.ndim == 1:
 103        points = points[np.newaxis, :]
 104
 105    if len(points[0]) == 2:
 106        return points, (0, 0, 1)
 107
 108    if n0 is None:  # fit plane
 109        datamean = points.mean(axis=0)
 110        vv = np.linalg.svd(points - datamean)[2]
 111        n0 = np.cross(vv[0], vv[1])
 112
 113    n0 = n0 / np.linalg.norm(n0)
 114    n1 = n1 / np.linalg.norm(n1)
 115    k = np.cross(n0, n1)
 116    l = np.linalg.norm(k)
 117    if not l:
 118        k = n0
 119    k /= np.linalg.norm(k)
 120
 121    ct = np.dot(n0, n1)
 122    theta = np.arccos(ct)
 123    st = np.sin(theta)
 124    v = k * (1 - ct)
 125
 126    rpoints = []
 127    for p in points:
 128        a = p * ct
 129        b = np.cross(k, p) * st
 130        c = v * np.dot(k, p)
 131        rpoints.append(a + b + c)
 132
 133    return np.array(rpoints), n0
 134
 135
 136def fit_line(points: Union[np.ndarray, "vedo.Points"]) -> "vedo.shapes.Line":
 137    """
 138    Fits a line through points.
 139
 140    Extra info is stored in `Line.slope`, `Line.center`, `Line.variances`.
 141
 142    Examples:
 143        - [fitline.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/fitline.py)
 144
 145            ![](https://vedo.embl.es/images/advanced/fitline.png)
 146    """
 147    if isinstance(points, Points):
 148        points = points.coordinates
 149    data = np.asarray(points)
 150    datamean = data.mean(axis=0)
 151    _, dd, vv = np.linalg.svd(data - datamean)
 152    vv = vv[0] / np.linalg.norm(vv[0])
 153    # vv contains the first principal component, i.e. the direction
 154    # vector of the best fit line in the least squares sense.
 155    xyz_min = data.min(axis=0)
 156    xyz_max = data.max(axis=0)
 157    a = np.linalg.norm(xyz_min - datamean)
 158    b = np.linalg.norm(xyz_max - datamean)
 159    p1 = datamean - a * vv
 160    p2 = datamean + b * vv
 161    line = vedo.shapes.Line(p1, p2, lw=1)
 162    line.slope = vv
 163    line.center = datamean
 164    line.variances = dd
 165    return line
 166
 167
 168def fit_circle(points: Union[np.ndarray, "vedo.Points"]) -> tuple:
 169    """
 170    Fits a circle through a set of 3D points, with a very fast non-iterative method.
 171
 172    Returns the tuple `(center, radius, normal_to_circle)`.
 173
 174    .. warning::
 175        trying to fit s-shaped points will inevitably lead to instabilities and
 176        circles of small radius.
 177
 178    References:
 179        *J.F. Crawford, Nucl. Instr. Meth. 211, 1983, 223-225.*
 180    """
 181    if isinstance(points, Points):
 182        points = points.coordinates
 183    data = np.asarray(points)
 184
 185    offs = data.mean(axis=0)
 186    data, n0 = _rotate_points(data - offs)
 187
 188    xi = data[:, 0]
 189    yi = data[:, 1]
 190
 191    x = sum(xi)
 192    xi2 = xi * xi
 193    xx = sum(xi2)
 194    xxx = sum(xi2 * xi)
 195
 196    y = sum(yi)
 197    yi2 = yi * yi
 198    yy = sum(yi2)
 199    yyy = sum(yi2 * yi)
 200
 201    xiyi = xi * yi
 202    xy = sum(xiyi)
 203    xyy = sum(xiyi * yi)
 204    xxy = sum(xi * xiyi)
 205
 206    N = len(xi)
 207    k = (xx + yy) / N
 208
 209    a1 = xx - x * x / N
 210    b1 = xy - x * y / N
 211    c1 = 0.5 * (xxx + xyy - x * k)
 212
 213    a2 = xy - x * y / N
 214    b2 = yy - y * y / N
 215    c2 = 0.5 * (xxy + yyy - y * k)
 216
 217    d = a2 * b1 - a1 * b2
 218    if not d:
 219        return offs, 0, n0
 220    x0 = (b1 * c2 - b2 * c1) / d
 221    y0 = (c1 - a1 * x0) / b1
 222
 223    R = np.sqrt(x0 * x0 + y0 * y0 - 1 / N * (2 * x0 * x + 2 * y0 * y - xx - yy))
 224
 225    c, _ = _rotate_points([x0, y0, 0], (0, 0, 1), n0)
 226
 227    return c[0] + offs, R, n0
 228
 229
 230def fit_plane(points: Union[np.ndarray, "vedo.Points"], signed=False) -> "vedo.shapes.Plane":
 231    """
 232    Fits a plane to a set of points.
 233
 234    Extra info is stored in `Plane.normal`, `Plane.center`, `Plane.variance`.
 235
 236    Arguments:
 237        signed : (bool)
 238            if True flip sign of the normal based on the ordering of the points
 239
 240    Examples:
 241        - [fitline.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/fitline.py)
 242
 243            ![](https://vedo.embl.es/images/advanced/fitline.png)
 244    """
 245    if isinstance(points, Points):
 246        points = points.coordinates
 247    data = np.asarray(points)
 248    datamean = data.mean(axis=0)
 249    pts = data - datamean
 250    res = np.linalg.svd(pts)
 251    dd, vv = res[1], res[2]
 252    n = np.cross(vv[0], vv[1])
 253    if signed:
 254        v = np.zeros_like(pts)
 255        for i in range(len(pts) - 1):
 256            vi = np.cross(pts[i], pts[i + 1])
 257            v[i] = vi / np.linalg.norm(vi)
 258        ns = np.mean(v, axis=0)  # normal to the points plane
 259        if np.dot(n, ns) < 0:
 260            n = -n
 261    xyz_min = data.min(axis=0)
 262    xyz_max = data.max(axis=0)
 263    s = np.linalg.norm(xyz_max - xyz_min)
 264    pla = vedo.shapes.Plane(datamean, n, s=[s, s])
 265    pla.variance = dd[2]
 266    pla.name = "FitPlane"
 267    return pla
 268
 269
 270def fit_sphere(coords: Union[np.ndarray, "vedo.Points"]) -> "vedo.shapes.Sphere":
 271    """
 272    Fits a sphere to a set of points.
 273
 274    Extra info is stored in `Sphere.radius`, `Sphere.center`, `Sphere.residue`.
 275
 276    Examples:
 277        - [fitspheres1.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/fitspheres1.py)
 278
 279            ![](https://vedo.embl.es/images/advanced/fitspheres1.jpg)
 280    """
 281    if isinstance(coords, Points):
 282        coords = coords.coordinates
 283    coords = np.array(coords)
 284    n = len(coords)
 285    A = np.zeros((n, 4))
 286    A[:, :-1] = coords * 2
 287    A[:, 3] = 1
 288    f = np.zeros((n, 1))
 289    x = coords[:, 0]
 290    y = coords[:, 1]
 291    z = coords[:, 2]
 292    f[:, 0] = x * x + y * y + z * z
 293    try:
 294        C, residue, rank, _ = np.linalg.lstsq(A, f, rcond=-1)  # solve AC=f
 295    except:
 296        C, residue, rank, _ = np.linalg.lstsq(A, f)  # solve AC=f
 297    if rank < 4:
 298        return None
 299    t = (C[0] * C[0]) + (C[1] * C[1]) + (C[2] * C[2]) + C[3]
 300    radius = np.sqrt(t)[0]
 301    center = np.array([C[0][0], C[1][0], C[2][0]])
 302    if len(residue) > 0:
 303        residue = np.sqrt(residue[0]) / n
 304    else:
 305        residue = 0
 306    sph = vedo.shapes.Sphere(center, radius, c=(1, 0, 0)).wireframe(1)
 307    sph.radius = radius
 308    sph.center = center
 309    sph.residue = residue
 310    sph.name = "FitSphere"
 311    return sph
 312
 313
 314def pca_ellipse(points: Union[np.ndarray, "vedo.Points"], pvalue=0.673, res=60) -> Union["vedo.shapes.Circle", None]:
 315    """
 316    Create the oriented 2D ellipse that contains the fraction `pvalue` of points.
 317    PCA (Principal Component Analysis) is used to compute the ellipse orientation.
 318
 319    Parameter `pvalue` sets the specified fraction of points inside the ellipse.
 320    Normalized directions are stored in `ellipse.axis1`, `ellipse.axis2`.
 321    Axes sizes are stored in `ellipse.va`, `ellipse.vb`
 322
 323    Arguments:
 324        pvalue : (float)
 325            ellipse will include this fraction of points
 326        res : (int)
 327            resolution of the ellipse
 328
 329    Examples:
 330        - [pca_ellipse.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/pca_ellipse.py)
 331        - [histo_pca.py](https://github.com/marcomusy/vedo/tree/master/examples/pyplot/histo_pca.py)
 332
 333 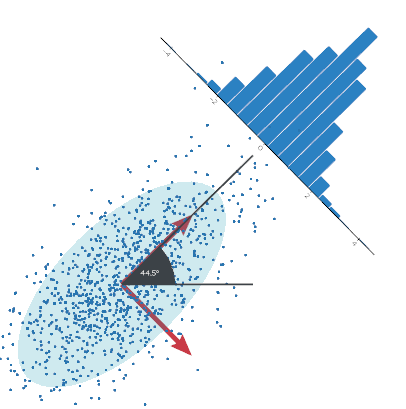           ![](https://vedo.embl.es/images/pyplot/histo_pca.png)
 334    """
 335    from scipy.stats import f
 336
 337    if isinstance(points, Points):
 338        coords = points.coordinates
 339    else:
 340        coords = points
 341    if len(coords) < 4:
 342        vedo.logger.warning("in pca_ellipse(), there are not enough points!")
 343        return None
 344
 345    P = np.array(coords, dtype=float)[:, (0, 1)]
 346    cov = np.cov(P, rowvar=0)      # type: ignore
 347    _, s, R = np.linalg.svd(cov)   # singular value decomposition
 348    p, n = s.size, P.shape[0]
 349    fppf = f.ppf(pvalue, p, n - p) # f % point function
 350    u = np.sqrt(s * fppf / 2) * 2  # semi-axes (largest first)
 351    ua, ub = u
 352    center = utils.make3d(np.mean(P, axis=0)) # centroid of the ellipse
 353
 354    t = LinearTransform(R.T * u).translate(center)
 355    elli = vedo.shapes.Circle(alpha=0.75, res=res)
 356    elli.apply_transform(t)
 357    elli.properties.LightingOff()
 358
 359    elli.pvalue = pvalue
 360    elli.center = np.array([center[0], center[1], 0])
 361    elli.nr_of_points = n
 362    elli.va = ua
 363    elli.vb = ub
 364
 365    # we subtract center because it's in t
 366    elli.axis1 = t.move([1, 0, 0]) - center
 367    elli.axis2 = t.move([0, 1, 0]) - center
 368
 369    elli.axis1 /= np.linalg.norm(elli.axis1)
 370    elli.axis2 /= np.linalg.norm(elli.axis2)
 371    elli.name = "PCAEllipse"
 372    return elli
 373
 374
 375def pca_ellipsoid(points: Union[np.ndarray, "vedo.Points"], pvalue=0.673, res=24) -> Union["vedo.shapes.Ellipsoid", None]:
 376    """
 377    Create the oriented ellipsoid that contains the fraction `pvalue` of points.
 378    PCA (Principal Component Analysis) is used to compute the ellipsoid orientation.
 379
 380    Axes sizes can be accessed in `ellips.va`, `ellips.vb`, `ellips.vc`,
 381    normalized directions are stored in `ellips.axis1`, `ellips.axis2` and `ellips.axis3`.
 382    Center of mass is stored in `ellips.center`.
 383
 384    Asphericity can be accessed in `ellips.asphericity()` and ellips.asphericity_error().
 385    A value of 0 means a perfect sphere.
 386
 387    Arguments:
 388        pvalue : (float)
 389            ellipsoid will include this fraction of points
 390
 391    Examples:
 392        [pca_ellipsoid.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/pca_ellipsoid.py)
 393
 394            ![](https://vedo.embl.es/images/basic/pca.png)
 395
 396    See also:
 397        `pca_ellipse()` for a 2D ellipse.
 398    """
 399    from scipy.stats import f
 400
 401    if isinstance(points, Points):
 402        coords = points.coordinates
 403    else:
 404        coords = points
 405    if len(coords) < 4:
 406        vedo.logger.warning("in pca_ellipsoid(), not enough input points!")
 407        return None
 408
 409    P = np.array(coords, ndmin=2, dtype=float)
 410    cov = np.cov(P, rowvar=0)     # type: ignore
 411    _, s, R = np.linalg.svd(cov)  # singular value decomposition
 412    p, n = s.size, P.shape[0]
 413    fppf = f.ppf(pvalue, p, n-p)*(n-1)*p*(n+1)/n/(n-p)  # f % point function
 414    u = np.sqrt(s*fppf)
 415    ua, ub, uc = u                # semi-axes (largest first)
 416    center = np.mean(P, axis=0)   # centroid of the hyperellipsoid
 417
 418    t = LinearTransform(R.T * u).translate(center)
 419    elli = vedo.shapes.Ellipsoid((0,0,0), (1,0,0), (0,1,0), (0,0,1), res=res)
 420    elli.apply_transform(t)
 421    elli.alpha(0.25)
 422    elli.properties.LightingOff()
 423
 424    elli.pvalue = pvalue
 425    elli.nr_of_points = n
 426    elli.center = center
 427    elli.va = ua
 428    elli.vb = ub
 429    elli.vc = uc
 430    # we subtract center because it's in t
 431    elli.axis1 = np.array(t.move([1, 0, 0])) - center
 432    elli.axis2 = np.array(t.move([0, 1, 0])) - center
 433    elli.axis3 = np.array(t.move([0, 0, 1])) - center
 434    elli.axis1 /= np.linalg.norm(elli.axis1)
 435    elli.axis2 /= np.linalg.norm(elli.axis2)
 436    elli.axis3 /= np.linalg.norm(elli.axis3)
 437    elli.name = "PCAEllipsoid"
 438    return elli
 439
 440
 441###################################################
 442def Point(pos=(0, 0, 0), r=12, c="red", alpha=1.0) -> Self:
 443    """
 444    Create a simple point in space.
 445
 446    .. note:: if you are creating many points you should use class `Points` instead!
 447    """
 448    pt = Points([[0,0,0]], r, c, alpha).pos(pos)
 449    pt.name = "Point"
 450    return pt
 451
 452
 453###################################################
 454class Points(PointsVisual, PointAlgorithms):
 455    """Work with point clouds."""
 456
 457    def __init__(self, inputobj=None, r=4, c=(0.2, 0.2, 0.2), alpha=1):
 458        """
 459        Build an object made of only vertex points for a list of 2D/3D points.
 460        Both shapes (N, 3) or (3, N) are accepted as input, if N>3.
 461
 462        Arguments:
 463            inputobj : (list, tuple)
 464            r : (int)
 465                Point radius in units of pixels.
 466            c : (str, list)
 467                Color name or rgb tuple.
 468            alpha : (float)
 469                Transparency in range [0,1].
 470
 471        Example:
 472            ```python
 473            from vedo import *
 474
 475            def fibonacci_sphere(n):
 476                s = np.linspace(0, n, num=n, endpoint=False)
 477                theta = s * 2.399963229728653
 478                y = 1 - s * (2/(n-1))
 479                r = np.sqrt(1 - y * y)
 480                x = np.cos(theta) * r
 481                z = np.sin(theta) * r
 482                return np._c[x,y,z]
 483
 484            Points(fibonacci_sphere(1000)).show(axes=1).close()
 485            ```
 486 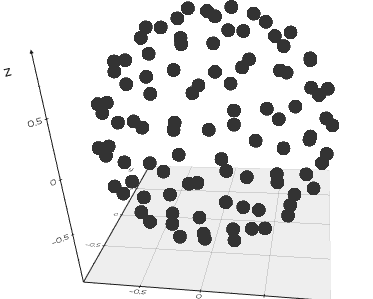           ![](https://vedo.embl.es/images/feats/fibonacci.png)
 487        """
 488        # print("INIT POINTS")
 489        super().__init__()
 490
 491        self.name = ""
 492        self.filename = ""
 493        self.file_size = ""
 494
 495        self.info = {}
 496        self.time = time.time()
 497
 498        self.transform = LinearTransform()
 499
 500        self.point_locator = None
 501        self.cell_locator = None
 502        self.line_locator = None
 503
 504        self.actor = vtki.vtkActor()
 505        self.properties = self.actor.GetProperty()
 506        self.properties_backface = self.actor.GetBackfaceProperty()
 507        self.mapper = vtki.new("PolyDataMapper")
 508        self.dataset = vtki.vtkPolyData()
 509
 510        # Create weakref so actor can access this object (eg to pick/remove):
 511        self.actor.retrieve_object = weak_ref_to(self)
 512
 513        try:
 514            self.properties.RenderPointsAsSpheresOn()
 515        except AttributeError:
 516            pass
 517
 518        if inputobj is None:  ####################
 519            return
 520        ##########################################
 521
 522        self.name = "Points"
 523
 524        ######
 525        if isinstance(inputobj, vtki.vtkActor):
 526            self.dataset.DeepCopy(inputobj.GetMapper().GetInput())
 527            pr = vtki.vtkProperty()
 528            pr.DeepCopy(inputobj.GetProperty())
 529            self.actor.SetProperty(pr)
 530            self.properties = pr
 531            self.mapper.SetScalarVisibility(inputobj.GetMapper().GetScalarVisibility())
 532
 533        elif isinstance(inputobj, vtki.vtkPolyData):
 534            self.dataset = inputobj
 535            if self.dataset.GetNumberOfCells() == 0:
 536                carr = vtki.vtkCellArray()
 537                for i in range(self.dataset.GetNumberOfPoints()):
 538                    carr.InsertNextCell(1)
 539                    carr.InsertCellPoint(i)
 540                self.dataset.SetVerts(carr)
 541
 542        elif isinstance(inputobj, Points):
 543            self.dataset = inputobj.dataset
 544            self.copy_properties_from(inputobj)
 545
 546        elif utils.is_sequence(inputobj):  # passing point coords
 547            self.dataset = utils.buildPolyData(utils.make3d(inputobj))
 548
 549        elif isinstance(inputobj, str) or "PosixPath" in str(type(inputobj)):
 550            verts = vedo.file_io.load(inputobj)
 551            self.filename = str(inputobj)
 552            self.dataset = verts.dataset
 553
 554        elif "meshlib" in str(type(inputobj)):
 555            from meshlib import mrmeshnumpy as mn
 556            self.dataset = utils.buildPolyData(mn.toNumpyArray(inputobj.points))
 557
 558        else:
 559            # try to extract the points from a generic VTK input data object
 560            if hasattr(inputobj, "dataset"):
 561                inputobj = inputobj.dataset
 562            try:
 563                vvpts = inputobj.GetPoints()
 564                self.dataset = vtki.vtkPolyData()
 565                self.dataset.SetPoints(vvpts)
 566                for i in range(inputobj.GetPointData().GetNumberOfArrays()):
 567                    arr = inputobj.GetPointData().GetArray(i)
 568                    self.dataset.GetPointData().AddArray(arr)
 569                carr = vtki.vtkCellArray()
 570                for i in range(self.dataset.GetNumberOfPoints()):
 571                    carr.InsertNextCell(1)
 572                    carr.InsertCellPoint(i)
 573                self.dataset.SetVerts(carr)
 574            except:
 575                vedo.logger.error(f"cannot build Points from type {type(inputobj)}")
 576                raise RuntimeError()
 577
 578        self.actor.SetMapper(self.mapper)
 579        self.mapper.SetInputData(self.dataset)
 580
 581        self.properties.SetColor(colors.get_color(c))
 582        self.properties.SetOpacity(alpha)
 583        self.properties.SetRepresentationToPoints()
 584        self.properties.SetPointSize(r)
 585        self.properties.LightingOff()
 586
 587        self.pipeline = utils.OperationNode(
 588            self, parents=[], comment=f"#pts {self.dataset.GetNumberOfPoints()}"
 589        )
 590
 591    def _update(self, polydata, reset_locators=True) -> Self:
 592        """Overwrite the polygonal dataset with a new vtkPolyData."""
 593        self.dataset = polydata
 594        self.mapper.SetInputData(self.dataset)
 595        self.mapper.Modified()
 596        if reset_locators:
 597            self.point_locator = None
 598            self.line_locator = None
 599            self.cell_locator = None
 600        return self
 601
 602    def __str__(self):
 603        """Print a description of the Points/Mesh."""
 604        module = self.__class__.__module__
 605        name = self.__class__.__name__
 606        out = vedo.printc(
 607            f"{module}.{name} at ({hex(self.memory_address())})".ljust(75),
 608            c="g", bold=True, invert=True, return_string=True,
 609        )
 610        out += "\x1b[0m\x1b[32;1m"
 611
 612        if self.name:
 613            out += "name".ljust(14) + ": " + self.name
 614            if "legend" in self.info.keys() and self.info["legend"]:
 615                out+= f", legend='{self.info['legend']}'"
 616            out += "\n"
 617
 618        if self.filename:
 619            out+= "file name".ljust(14) + ": " + self.filename + "\n"
 620
 621        if not self.mapper.GetScalarVisibility():
 622            col = utils.precision(self.properties.GetColor(), 3)
 623            cname = vedo.colors.get_color_name(self.properties.GetColor())
 624            out+= "color".ljust(14) + ": " + cname
 625            out+= f", rgb={col}, alpha={self.properties.GetOpacity()}\n"
 626            if self.actor.GetBackfaceProperty():
 627                bcol = self.actor.GetBackfaceProperty().GetDiffuseColor()
 628                cname = vedo.colors.get_color_name(bcol)
 629                out+= "backface color".ljust(14) + ": "
 630                out+= f"{cname}, rgb={utils.precision(bcol,3)}\n"
 631
 632        npt = self.dataset.GetNumberOfPoints()
 633        npo, nln = self.dataset.GetNumberOfPolys(), self.dataset.GetNumberOfLines()
 634        out+= "elements".ljust(14) + f": vertices={npt:,} polygons={npo:,} lines={nln:,}"
 635        if self.dataset.GetNumberOfStrips():
 636            out+= f", strips={self.dataset.GetNumberOfStrips():,}"
 637        out+= "\n"
 638        if self.dataset.GetNumberOfPieces() > 1:
 639            out+= "pieces".ljust(14) + ": " + str(self.dataset.GetNumberOfPieces()) + "\n"
 640
 641        out+= "position".ljust(14) + ": " + f"{utils.precision(self.pos(), 6)}\n"
 642        try:
 643            sc = self.transform.get_scale()
 644            out+= "scaling".ljust(14)  + ": "
 645            out+= utils.precision(sc, 6) + "\n"
 646        except AttributeError:
 647            pass
 648
 649        if self.npoints:
 650            out+="size".ljust(14)+ ": average=" + utils.precision(self.average_size(),6)
 651            out+=", diagonal="+ utils.precision(self.diagonal_size(), 6)+ "\n"
 652            out+="center of mass".ljust(14) + ": " + utils.precision(self.center_of_mass(),6)+"\n"
 653
 654        bnds = self.bounds()
 655        bx1, bx2 = utils.precision(bnds[0], 3), utils.precision(bnds[1], 3)
 656        by1, by2 = utils.precision(bnds[2], 3), utils.precision(bnds[3], 3)
 657        bz1, bz2 = utils.precision(bnds[4], 3), utils.precision(bnds[5], 3)
 658        out+= "bounds".ljust(14) + ":"
 659        out+= " x=(" + bx1 + ", " + bx2 + "),"
 660        out+= " y=(" + by1 + ", " + by2 + "),"
 661        out+= " z=(" + bz1 + ", " + bz2 + ")\n"
 662
 663        for key in self.pointdata.keys():
 664            arr = self.pointdata[key]
 665            dim = arr.shape[1] if arr.ndim > 1 else 1
 666            mark_active = "pointdata"
 667            a_scalars = self.dataset.GetPointData().GetScalars()
 668            a_vectors = self.dataset.GetPointData().GetVectors()
 669            a_tensors = self.dataset.GetPointData().GetTensors()
 670            if   a_scalars and a_scalars.GetName() == key:
 671                mark_active += " *"
 672            elif a_vectors and a_vectors.GetName() == key:
 673                mark_active += " **"
 674            elif a_tensors and a_tensors.GetName() == key:
 675                mark_active += " ***"
 676            out += mark_active.ljust(14) + f': "{key}" ({arr.dtype}), dim={dim}'
 677            if dim == 1 and len(arr)>0:
 678                rng = utils.precision(arr.min(), 3) + ", " + utils.precision(arr.max(), 3)
 679                out += f", range=({rng})\n"
 680            else:
 681                out += "\n"
 682
 683        for key in self.celldata.keys():
 684            arr = self.celldata[key]
 685            dim = arr.shape[1] if arr.ndim > 1 else 1
 686            mark_active = "celldata"
 687            a_scalars = self.dataset.GetCellData().GetScalars()
 688            a_vectors = self.dataset.GetCellData().GetVectors()
 689            a_tensors = self.dataset.GetCellData().GetTensors()
 690            if   a_scalars and a_scalars.GetName() == key:
 691                mark_active += " *"
 692            elif a_vectors and a_vectors.GetName() == key:
 693                mark_active += " **"
 694            elif a_tensors and a_tensors.GetName() == key:
 695                mark_active += " ***"
 696            out += mark_active.ljust(14) + f': "{key}" ({arr.dtype}), dim={dim}'
 697            if dim == 1 and len(arr)>0:
 698                rng = utils.precision(arr.min(), 3) + ", " + utils.precision(arr.max(), 3)
 699                out += f", range=({rng})\n"
 700            else:
 701                out += "\n"
 702
 703        for key in self.metadata.keys():
 704            arr = self.metadata[key]
 705            if len(arr) > 3:
 706                out+= "metadata".ljust(14) + ": " + f'"{key}" ({len(arr)} values)\n'
 707            else:
 708                out+= "metadata".ljust(14) + ": " + f'"{key}" = {arr}\n'
 709
 710        if self.picked3d is not None:
 711            idp = self.closest_point(self.picked3d, return_point_id=True)
 712            idc = self.closest_point(self.picked3d, return_cell_id=True)
 713            out+= "clicked point".ljust(14) + ": " + utils.precision(self.picked3d, 6)
 714            out+= f", pointID={idp}, cellID={idc}\n"
 715
 716        return out.rstrip() + "\x1b[0m"
 717
 718    def _repr_html_(self):
 719        """
 720        HTML representation of the Point cloud object for Jupyter Notebooks.
 721
 722        Returns:
 723            HTML text with the image and some properties.
 724        """
 725        import io
 726        import base64
 727        from PIL import Image
 728
 729        library_name = "vedo.pointcloud.Points"
 730        help_url = "https://vedo.embl.es/docs/vedo/pointcloud.html#Points"
 731
 732        arr = self.thumbnail()
 733        im = Image.fromarray(arr)
 734        buffered = io.BytesIO()
 735        im.save(buffered, format="PNG", quality=100)
 736        encoded = base64.b64encode(buffered.getvalue()).decode("utf-8")
 737        url = "data:image/png;base64," + encoded
 738        image = f"<img src='{url}'></img>"
 739
 740        bounds = "<br/>".join(
 741            [
 742                utils.precision(min_x, 4) + " ... " + utils.precision(max_x, 4)
 743                for min_x, max_x in zip(self.bounds()[::2], self.bounds()[1::2])
 744            ]
 745        )
 746        average_size = "{size:.3f}".format(size=self.average_size())
 747
 748        help_text = ""
 749        if self.name:
 750            help_text += f"<b> {self.name}: &nbsp&nbsp</b>"
 751        help_text += '<b><a href="' + help_url + '" target="_blank">' + library_name + "</a></b>"
 752        if self.filename:
 753            dots = ""
 754            if len(self.filename) > 30:
 755                dots = "..."
 756            help_text += f"<br/><code><i>({dots}{self.filename[-30:]})</i></code>"
 757
 758        pdata = ""
 759        if self.dataset.GetPointData().GetScalars():
 760            if self.dataset.GetPointData().GetScalars().GetName():
 761                name = self.dataset.GetPointData().GetScalars().GetName()
 762                pdata = "<tr><td><b> point data array </b></td><td>" + name + "</td></tr>"
 763
 764        cdata = ""
 765        if self.dataset.GetCellData().GetScalars():
 766            if self.dataset.GetCellData().GetScalars().GetName():
 767                name = self.dataset.GetCellData().GetScalars().GetName()
 768                cdata = "<tr><td><b> cell data array </b></td><td>" + name + "</td></tr>"
 769
 770        allt = [
 771            "<table>",
 772            "<tr>",
 773            "<td>",
 774            image,
 775            "</td>",
 776            "<td style='text-align: center; vertical-align: center;'><br/>",
 777            help_text,
 778            "<table>",
 779            "<tr><td><b> bounds </b> <br/> (x/y/z) </td><td>" + str(bounds) + "</td></tr>",
 780            "<tr><td><b> center of mass </b></td><td>"
 781            + utils.precision(self.center_of_mass(), 3)
 782            + "</td></tr>",
 783            "<tr><td><b> average size </b></td><td>" + str(average_size) + "</td></tr>",
 784            "<tr><td><b> nr. points </b></td><td>" + str(self.npoints) + "</td></tr>",
 785            pdata,
 786            cdata,
 787            "</table>",
 788            "</table>",
 789        ]
 790        return "\n".join(allt)
 791
 792    ##################################################################################
 793    def __add__(self, meshs):
 794        """
 795        Add two meshes or a list of meshes together to form an `Assembly` object.
 796        """
 797        if isinstance(meshs, list):
 798            alist = [self]
 799            for l in meshs:
 800                if isinstance(l, vedo.Assembly):
 801                    alist += l.unpack()
 802                else:
 803                    alist += l
 804            return vedo.assembly.Assembly(alist)
 805
 806        if isinstance(meshs, vedo.Assembly):
 807            return meshs + self  # use Assembly.__add__
 808
 809        return vedo.assembly.Assembly([self, meshs])
 810
 811    def polydata(self):
 812        """
 813        Obsolete. Use property `.dataset` instead.
 814        Returns the underlying `vtkPolyData` object.
 815        """
 816        colors.printc(
 817            "WARNING: call to .polydata() is obsolete, use property .dataset instead.",
 818            c="y")
 819        return self.dataset
 820
 821    def __copy__(self):
 822        return self.clone(deep=False)
 823
 824    def __deepcopy__(self, memo):
 825        return self.clone(deep=memo)
 826
 827    def copy(self, deep=True) -> Self:
 828        """Return a copy of the object. Alias of `clone()`."""
 829        return self.clone(deep=deep)
 830
 831    def clone(self, deep=True) -> Self:
 832        """
 833        Clone a `PointCloud` or `Mesh` object to make an exact copy of it.
 834        Alias of `copy()`.
 835
 836        Arguments:
 837            deep : (bool)
 838                if False return a shallow copy of the mesh without copying the points array.
 839
 840        Examples:
 841            - [mirror.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/mirror.py)
 842
 843               ![](https://vedo.embl.es/images/basic/mirror.png)
 844        """
 845        poly = vtki.vtkPolyData()
 846        if deep or isinstance(deep, dict): # if a memo object is passed this checks as True
 847            poly.DeepCopy(self.dataset)
 848        else:
 849            poly.ShallowCopy(self.dataset)
 850
 851        if isinstance(self, vedo.Mesh):
 852            cloned = vedo.Mesh(poly)
 853        else:
 854            cloned = Points(poly)
 855        # print([self], self.__class__)
 856        # cloned = self.__class__(poly)
 857
 858        cloned.transform = self.transform.clone()
 859
 860        cloned.copy_properties_from(self)
 861
 862        cloned.name = str(self.name)
 863        cloned.filename = str(self.filename)
 864        cloned.info = dict(self.info)
 865        cloned.pipeline = utils.OperationNode("clone", parents=[self], shape="diamond", c="#edede9")
 866
 867        if isinstance(deep, dict):
 868            deep[id(self)] = cloned
 869
 870        return cloned
 871
 872    def compute_normals_with_pca(self, n=20, orientation_point=None, invert=False) -> Self:
 873        """
 874        Generate point normals using PCA (principal component analysis).
 875        This algorithm estimates a local tangent plane around each sample point p
 876        by considering a small neighborhood of points around p, and fitting a plane
 877        to the neighborhood (via PCA).
 878
 879        Arguments:
 880            n : (int)
 881                neighborhood size to calculate the normal
 882            orientation_point : (list)
 883                adjust the +/- sign of the normals so that
 884                the normals all point towards a specified point. If None, perform a traversal
 885                of the point cloud and flip neighboring normals so that they are mutually consistent.
 886            invert : (bool)
 887                flip all normals
 888        """
 889        poly = self.dataset
 890        pcan = vtki.new("PCANormalEstimation")
 891        pcan.SetInputData(poly)
 892        pcan.SetSampleSize(n)
 893
 894        if orientation_point is not None:
 895            pcan.SetNormalOrientationToPoint()
 896            pcan.SetOrientationPoint(orientation_point)
 897        else:
 898            pcan.SetNormalOrientationToGraphTraversal()
 899
 900        if invert:
 901            pcan.FlipNormalsOn()
 902        pcan.Update()
 903
 904        varr = pcan.GetOutput().GetPointData().GetNormals()
 905        varr.SetName("Normals")
 906        self.dataset.GetPointData().SetNormals(varr)
 907        self.dataset.GetPointData().Modified()
 908        return self
 909
 910    def compute_acoplanarity(self, n=25, radius=None, on="points") -> Self:
 911        """
 912        Compute acoplanarity which is a measure of how much a local region of the mesh
 913        differs from a plane.
 914
 915        The information is stored in a `pointdata` or `celldata` array with name 'Acoplanarity'.
 916
 917        Either `n` (number of neighbour points) or `radius` (radius of local search) can be specified.
 918        If a radius value is given and not enough points fall inside it, then a -1 is stored.
 919
 920        Example:
 921            ```python
 922            from vedo import *
 923            msh = ParametricShape('RandomHills')
 924            msh.compute_acoplanarity(radius=0.1, on='cells')
 925            msh.cmap("coolwarm", on='cells').add_scalarbar()
 926            msh.show(axes=1).close()
 927            ```
 928 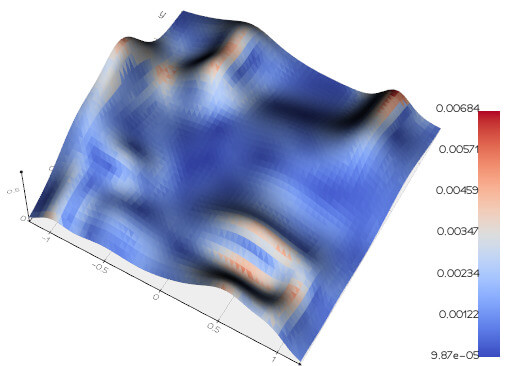           ![](https://vedo.embl.es/images/feats/acoplanarity.jpg)
 929        """
 930        acoplanarities = []
 931        if "point" in on:
 932            pts = self.coordinates
 933        elif "cell" in on:
 934            pts = self.cell_centers().coordinates
 935        else:
 936            raise ValueError(f"In compute_acoplanarity() set on to either 'cells' or 'points', not {on}")
 937
 938        for p in utils.progressbar(pts, delay=5, width=15, title=f"{on} acoplanarity"):
 939            if n:
 940                data = self.closest_point(p, n=n)
 941                npts = n
 942            elif radius:
 943                data = self.closest_point(p, radius=radius)
 944                npts = len(data)
 945
 946            try:
 947                center = data.mean(axis=0)
 948                res = np.linalg.svd(data - center)
 949                acoplanarities.append(res[1][2] / npts)
 950            except:
 951                acoplanarities.append(-1.0)
 952
 953        if "point" in on:
 954            self.pointdata["Acoplanarity"] = np.array(acoplanarities, dtype=float)
 955        else:
 956            self.celldata["Acoplanarity"] = np.array(acoplanarities, dtype=float)
 957        return self
 958
 959    def distance_to(self, pcloud, signed=False, invert=False, name="Distance") -> np.ndarray:
 960        """
 961        Computes the distance from one point cloud or mesh to another point cloud or mesh.
 962        This new `pointdata` array is saved with default name "Distance".
 963
 964        Keywords `signed` and `invert` are used to compute signed distance,
 965        but the mesh in that case must have polygonal faces (not a simple point cloud),
 966        and normals must also be computed.
 967
 968        Examples:
 969            - [distance2mesh.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/distance2mesh.py)
 970
 971 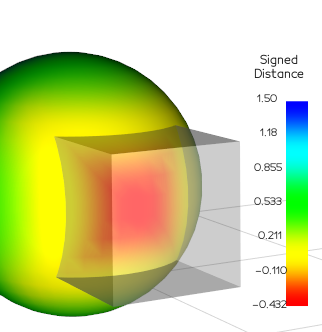               ![](https://vedo.embl.es/images/basic/distance2mesh.png)
 972        """
 973        if pcloud.dataset.GetNumberOfPolys():
 974
 975            poly1 = self.dataset
 976            poly2 = pcloud.dataset
 977            df = vtki.new("DistancePolyDataFilter")
 978            df.ComputeSecondDistanceOff()
 979            df.SetInputData(0, poly1)
 980            df.SetInputData(1, poly2)
 981            df.SetSignedDistance(signed)
 982            df.SetNegateDistance(invert)
 983            df.Update()
 984            scals = df.GetOutput().GetPointData().GetScalars()
 985            dists = utils.vtk2numpy(scals)
 986
 987        else:  # has no polygons
 988
 989            if signed:
 990                vedo.logger.warning("distance_to() called with signed=True but input object has no polygons")
 991
 992            if not pcloud.point_locator:
 993                pcloud.point_locator = vtki.new("PointLocator")
 994                pcloud.point_locator.SetDataSet(pcloud.dataset)
 995                pcloud.point_locator.BuildLocator()
 996
 997            ids = []
 998            ps1 = self.coordinates
 999            ps2 = pcloud.coordinates
1000            for p in ps1:
1001                pid = pcloud.point_locator.FindClosestPoint(p)
1002                ids.append(pid)
1003
1004            deltas = ps2[ids] - ps1
1005            dists = np.linalg.norm(deltas, axis=1).astype(np.float32)
1006            scals = utils.numpy2vtk(dists)
1007
1008        scals.SetName(name)
1009        self.dataset.GetPointData().AddArray(scals)
1010        self.dataset.GetPointData().SetActiveScalars(scals.GetName())
1011        rng = scals.GetRange()
1012        self.mapper.SetScalarRange(rng[0], rng[1])
1013        self.mapper.ScalarVisibilityOn()
1014
1015        self.pipeline = utils.OperationNode(
1016            "distance_to",
1017            parents=[self, pcloud],
1018            shape="cylinder",
1019            comment=f"#pts {self.dataset.GetNumberOfPoints()}",
1020        )
1021        return dists
1022
1023    def clean(self) -> Self:
1024        """Clean pointcloud or mesh by removing coincident points."""
1025        cpd = vtki.new("CleanPolyData")
1026        cpd.PointMergingOn()
1027        cpd.ConvertLinesToPointsOff()
1028        cpd.ConvertPolysToLinesOff()
1029        cpd.ConvertStripsToPolysOff()
1030        cpd.SetInputData(self.dataset)
1031        cpd.Update()
1032        self._update(cpd.GetOutput())
1033        self.pipeline = utils.OperationNode(
1034            "clean", parents=[self], comment=f"#pts {self.dataset.GetNumberOfPoints()}"
1035        )
1036        return self
1037
1038    def subsample(self, fraction: float, absolute=False) -> Self:
1039        """
1040        Subsample a point cloud by requiring that the points
1041        or vertices are far apart at least by the specified fraction of the object size.
1042        If a Mesh is passed the polygonal faces are not removed
1043        but holes can appear as their vertices are removed.
1044
1045        Examples:
1046            - [moving_least_squares1D.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/moving_least_squares1D.py)
1047
1048                ![](https://vedo.embl.es/images/advanced/moving_least_squares1D.png)
1049
1050            - [recosurface.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/recosurface.py)
1051
1052                ![](https://vedo.embl.es/images/advanced/recosurface.png)
1053        """
1054        if not absolute:
1055            if fraction > 1:
1056                vedo.logger.warning(
1057                    f"subsample(fraction=...), fraction must be < 1, but is {fraction}"
1058                )
1059            if fraction <= 0:
1060                return self
1061
1062        cpd = vtki.new("CleanPolyData")
1063        cpd.PointMergingOn()
1064        cpd.ConvertLinesToPointsOn()
1065        cpd.ConvertPolysToLinesOn()
1066        cpd.ConvertStripsToPolysOn()
1067        cpd.SetInputData(self.dataset)
1068        if absolute:
1069            cpd.SetTolerance(fraction / self.diagonal_size())
1070            # cpd.SetToleranceIsAbsolute(absolute)
1071        else:
1072            cpd.SetTolerance(fraction)
1073        cpd.Update()
1074
1075        ps = 2
1076        if self.properties.GetRepresentation() == 0:
1077            ps = self.properties.GetPointSize()
1078
1079        self._update(cpd.GetOutput())
1080        self.ps(ps)
1081
1082        self.pipeline = utils.OperationNode(
1083            "subsample", parents=[self], comment=f"#pts {self.dataset.GetNumberOfPoints()}"
1084        )
1085        return self
1086
1087    def threshold(self, scalars: str, above=None, below=None, on="points") -> Self:
1088        """
1089        Extracts cells where scalar value satisfies threshold criterion.
1090
1091        Arguments:
1092            scalars : (str)
1093                name of the scalars array.
1094            above : (float)
1095                minimum value of the scalar
1096            below : (float)
1097                maximum value of the scalar
1098            on : (str)
1099                if 'cells' assume array of scalars refers to cell data.
1100
1101        Examples:
1102            - [mesh_threshold.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/mesh_threshold.py)
1103        """
1104        thres = vtki.new("Threshold")
1105        thres.SetInputData(self.dataset)
1106
1107        if on.startswith("c"):
1108            asso = vtki.vtkDataObject.FIELD_ASSOCIATION_CELLS
1109        else:
1110            asso = vtki.vtkDataObject.FIELD_ASSOCIATION_POINTS
1111
1112        thres.SetInputArrayToProcess(0, 0, 0, asso, scalars)
1113
1114        if above is None and below is not None:
1115            try:  # vtk 9.2
1116                thres.ThresholdByLower(below)
1117            except AttributeError:  # vtk 9.3
1118                thres.SetUpperThreshold(below)
1119
1120        elif below is None and above is not None:
1121            try:
1122                thres.ThresholdByUpper(above)
1123            except AttributeError:
1124                thres.SetLowerThreshold(above)
1125        else:
1126            try:
1127                thres.ThresholdBetween(above, below)
1128            except AttributeError:
1129                thres.SetUpperThreshold(below)
1130                thres.SetLowerThreshold(above)
1131
1132        thres.Update()
1133
1134        gf = vtki.new("GeometryFilter")
1135        gf.SetInputData(thres.GetOutput())
1136        gf.Update()
1137        self._update(gf.GetOutput())
1138        self.pipeline = utils.OperationNode("threshold", parents=[self])
1139        return self
1140
1141    def quantize(self, value: float) -> Self:
1142        """
1143        The user should input a value and all {x,y,z} coordinates
1144        will be quantized to that absolute grain size.
1145        """
1146        qp = vtki.new("QuantizePolyDataPoints")
1147        qp.SetInputData(self.dataset)
1148        qp.SetQFactor(value)
1149        qp.Update()
1150        self._update(qp.GetOutput())
1151        self.pipeline = utils.OperationNode("quantize", parents=[self])
1152        return self
1153
1154    @property
1155    def vertex_normals(self) -> np.ndarray:
1156        """
1157        Retrieve vertex normals as a numpy array. Same as `point_normals`.
1158        If needed, normals are computed via `compute_normals_with_pca()`.
1159        Check out also `compute_normals()` and `compute_normals_with_pca()`.
1160        """
1161        vtknormals = self.dataset.GetPointData().GetNormals()
1162        if vtknormals is None:
1163            self.compute_normals_with_pca()
1164            vtknormals = self.dataset.GetPointData().GetNormals()
1165        return utils.vtk2numpy(vtknormals)
1166
1167    @property
1168    def point_normals(self) -> np.ndarray:
1169        """
1170        Retrieve vertex normals as a numpy array. Same as `vertex_normals`.
1171        Check out also `compute_normals()` and `compute_normals_with_pca()`.
1172        """
1173        return self.vertex_normals
1174
1175    def align_to(self, target, iters=100, rigid=False, invert=False, use_centroids=False) -> Self:
1176        """
1177        Aligned to target mesh through the `Iterative Closest Point` algorithm.
1178
1179        The core of the algorithm is to match each vertex in one surface with
1180        the closest surface point on the other, then apply the transformation
1181        that modify one surface to best match the other (in the least-square sense).
1182
1183        Arguments:
1184            rigid : (bool)
1185                if True do not allow scaling
1186            invert : (bool)
1187                if True start by aligning the target to the source but
1188                invert the transformation finally. Useful when the target is smaller
1189                than the source.
1190            use_centroids : (bool)
1191                start by matching the centroids of the two objects.
1192
1193        Examples:
1194            - [align1.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/align1.py)
1195
1196 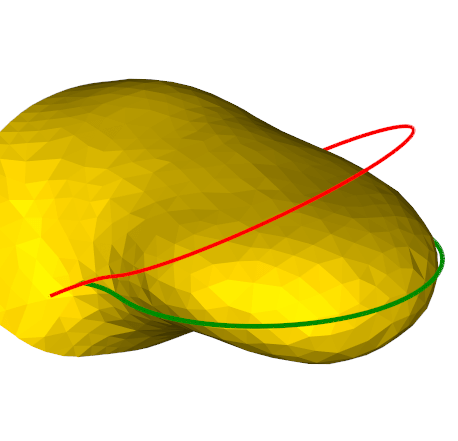               ![](https://vedo.embl.es/images/basic/align1.png)
1197
1198            - [align2.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/align2.py)
1199
1200                ![](https://vedo.embl.es/images/basic/align2.png)
1201        """
1202        icp = vtki.new("IterativeClosestPointTransform")
1203        icp.SetSource(self.dataset)
1204        icp.SetTarget(target.dataset)
1205        if invert:
1206            icp.Inverse()
1207        icp.SetMaximumNumberOfIterations(iters)
1208        if rigid:
1209            icp.GetLandmarkTransform().SetModeToRigidBody()
1210        icp.SetStartByMatchingCentroids(use_centroids)
1211        icp.Update()
1212
1213        self.apply_transform(icp.GetMatrix())
1214
1215        self.pipeline = utils.OperationNode(
1216            "align_to", parents=[self, target], comment=f"rigid = {rigid}"
1217        )
1218        return self
1219
1220    def align_to_bounding_box(self, msh, rigid=False) -> Self:
1221        """
1222        Align the current object's bounding box to the bounding box
1223        of the input object.
1224
1225        Use `rigid=True` to disable scaling.
1226
1227        Example:
1228            [align6.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/align6.py)
1229        """
1230        lmt = vtki.vtkLandmarkTransform()
1231        ss = vtki.vtkPoints()
1232        xss0, xss1, yss0, yss1, zss0, zss1 = self.bounds()
1233        for p in [
1234            [xss0, yss0, zss0],
1235            [xss1, yss0, zss0],
1236            [xss1, yss1, zss0],
1237            [xss0, yss1, zss0],
1238            [xss0, yss0, zss1],
1239            [xss1, yss0, zss1],
1240            [xss1, yss1, zss1],
1241            [xss0, yss1, zss1],
1242        ]:
1243            ss.InsertNextPoint(p)
1244        st = vtki.vtkPoints()
1245        xst0, xst1, yst0, yst1, zst0, zst1 = msh.bounds()
1246        for p in [
1247            [xst0, yst0, zst0],
1248            [xst1, yst0, zst0],
1249            [xst1, yst1, zst0],
1250            [xst0, yst1, zst0],
1251            [xst0, yst0, zst1],
1252            [xst1, yst0, zst1],
1253            [xst1, yst1, zst1],
1254            [xst0, yst1, zst1],
1255        ]:
1256            st.InsertNextPoint(p)
1257
1258        lmt.SetSourceLandmarks(ss)
1259        lmt.SetTargetLandmarks(st)
1260        lmt.SetModeToAffine()
1261        if rigid:
1262            lmt.SetModeToRigidBody()
1263        lmt.Update()
1264
1265        LT = LinearTransform(lmt)
1266        self.apply_transform(LT)
1267        return self
1268
1269    def align_with_landmarks(
1270        self,
1271        source_landmarks,
1272        target_landmarks,
1273        rigid=False,
1274        affine=False,
1275        least_squares=False,
1276    ) -> Self:
1277        """
1278        Transform mesh orientation and position based on a set of landmarks points.
1279        The algorithm finds the best matching of source points to target points
1280        in the mean least square sense, in one single step.
1281
1282        If `affine` is True the x, y and z axes can scale independently but stay collinear.
1283        With least_squares they can vary orientation.
1284
1285        Examples:
1286            - [align5.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/align5.py)
1287
1288 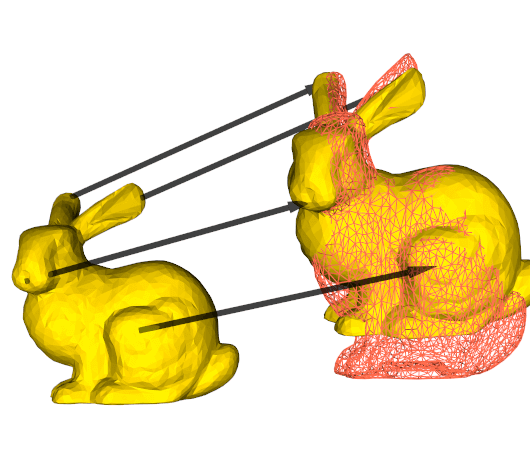               ![](https://vedo.embl.es/images/basic/align5.png)
1289        """
1290
1291        if utils.is_sequence(source_landmarks):
1292            ss = vtki.vtkPoints()
1293            for p in source_landmarks:
1294                ss.InsertNextPoint(p)
1295        else:
1296            ss = source_landmarks.dataset.GetPoints()
1297            if least_squares:
1298                source_landmarks = source_landmarks.coordinates
1299
1300        if utils.is_sequence(target_landmarks):
1301            st = vtki.vtkPoints()
1302            for p in target_landmarks:
1303                st.InsertNextPoint(p)
1304        else:
1305            st = target_landmarks.GetPoints()
1306            if least_squares:
1307                target_landmarks = target_landmarks.coordinates
1308
1309        if ss.GetNumberOfPoints() != st.GetNumberOfPoints():
1310            n1 = ss.GetNumberOfPoints()
1311            n2 = st.GetNumberOfPoints()
1312            vedo.logger.error(f"source and target have different nr of points {n1} vs {n2}")
1313            raise RuntimeError()
1314
1315        if int(rigid) + int(affine) + int(least_squares) > 1:
1316            vedo.logger.error(
1317                "only one of rigid, affine, least_squares can be True at a time"
1318            )
1319            raise RuntimeError()
1320
1321        lmt = vtki.vtkLandmarkTransform()
1322        lmt.SetSourceLandmarks(ss)
1323        lmt.SetTargetLandmarks(st)
1324        lmt.SetModeToSimilarity()
1325
1326        if rigid:
1327            lmt.SetModeToRigidBody()
1328            lmt.Update()
1329
1330        elif affine:
1331            lmt.SetModeToAffine()
1332            lmt.Update()
1333
1334        elif least_squares:
1335            cms = source_landmarks.mean(axis=0)
1336            cmt = target_landmarks.mean(axis=0)
1337            m = np.linalg.lstsq(source_landmarks - cms, target_landmarks - cmt, rcond=None)[0]
1338            M = vtki.vtkMatrix4x4()
1339            for i in range(3):
1340                for j in range(3):
1341                    M.SetElement(j, i, m[i][j])
1342            lmt = vtki.vtkTransform()
1343            lmt.Translate(cmt)
1344            lmt.Concatenate(M)
1345            lmt.Translate(-cms)
1346
1347        else:
1348            lmt.Update()
1349
1350        self.apply_transform(lmt)
1351        self.pipeline = utils.OperationNode("transform_with_landmarks", parents=[self])
1352        return self
1353
1354    def normalize(self) -> Self:
1355        """Scale average size to unit. The scaling is performed around the center of mass."""
1356        coords = self.coordinates
1357        if not coords.shape[0]:
1358            return self
1359        cm = np.mean(coords, axis=0)
1360        pts = coords - cm
1361        xyz2 = np.sum(pts * pts, axis=0)
1362        scale = 1 / np.sqrt(np.sum(xyz2) / len(pts))
1363        self.scale(scale, origin=cm)
1364        self.pipeline = utils.OperationNode("normalize", parents=[self])
1365        return self
1366
1367    def mirror(self, axis="x", origin=True) -> Self:
1368        """
1369        Mirror reflect along one of the cartesian axes
1370
1371        Arguments:
1372            axis : (str)
1373                axis to use for mirroring, must be set to `x, y, z`.
1374                Or any combination of those.
1375            origin : (list)
1376                use this point as the origin of the mirroring transformation.
1377
1378        Examples:
1379            - [mirror.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/mirror.py)
1380
1381                ![](https://vedo.embl.es/images/basic/mirror.png)
1382        """
1383        sx, sy, sz = 1, 1, 1
1384        if "x" in axis.lower(): sx = -1
1385        if "y" in axis.lower(): sy = -1
1386        if "z" in axis.lower(): sz = -1
1387
1388        self.scale([sx, sy, sz], origin=origin)
1389
1390        self.pipeline = utils.OperationNode(
1391            "mirror", comment=f"axis = {axis}", parents=[self])
1392
1393        if sx * sy * sz < 0:
1394            if hasattr(self, "reverse"):
1395                self.reverse()
1396        return self
1397
1398    def flip_normals(self) -> Self:
1399        """Flip all normals orientation."""
1400        rs = vtki.new("ReverseSense")
1401        rs.SetInputData(self.dataset)
1402        rs.ReverseCellsOff()
1403        rs.ReverseNormalsOn()
1404        rs.Update()
1405        self._update(rs.GetOutput())
1406        self.pipeline = utils.OperationNode("flip_normals", parents=[self])
1407        return self
1408
1409    def add_gaussian_noise(self, sigma=1.0) -> Self:
1410        """
1411        Add gaussian noise to point positions.
1412        An extra array is added named "GaussianNoise" with the displacements.
1413
1414        Arguments:
1415            sigma : (float)
1416                nr. of standard deviations, expressed in percent of the diagonal size of mesh.
1417                Can also be a list `[sigma_x, sigma_y, sigma_z]`.
1418
1419        Example:
1420            ```python
1421            from vedo import Sphere
1422            Sphere().add_gaussian_noise(1.0).point_size(8).show().close()
1423            ```
1424        """
1425        sz = self.diagonal_size()
1426        pts = self.coordinates
1427        n = len(pts)
1428        ns = (np.random.randn(n, 3) * sigma) * (sz / 100)
1429        vpts = vtki.vtkPoints()
1430        vpts.SetNumberOfPoints(n)
1431        vpts.SetData(utils.numpy2vtk(pts + ns, dtype=np.float32))
1432        self.dataset.SetPoints(vpts)
1433        self.dataset.GetPoints().Modified()
1434        self.pointdata["GaussianNoise"] = -ns
1435        self.pipeline = utils.OperationNode(
1436            "gaussian_noise", parents=[self], shape="egg", comment=f"sigma = {sigma}"
1437        )
1438        return self
1439
1440    def closest_point(
1441        self, pt, n=1, radius=None, return_point_id=False, return_cell_id=False
1442    ) -> Union[List[int], int, np.ndarray]:
1443        """
1444        Find the closest point(s) on a mesh given from the input point `pt`.
1445
1446        Arguments:
1447            n : (int)
1448                if greater than 1, return a list of n ordered closest points
1449            radius : (float)
1450                if given, get all points within that radius. Then n is ignored.
1451            return_point_id : (bool)
1452                return point ID instead of coordinates
1453            return_cell_id : (bool)
1454                return cell ID in which the closest point sits
1455
1456        Examples:
1457            - [align1.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/align1.py)
1458            - [fitplanes.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/fitplanes.py)
1459            - [quadratic_morphing.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/quadratic_morphing.py)
1460
1461        .. note::
1462            The appropriate tree search locator is built on the fly and cached for speed.
1463
1464            If you want to reset it use `mymesh.point_locator=None`
1465            and / or `mymesh.cell_locator=None`.
1466        """
1467        if len(pt) != 3:
1468            pt = [pt[0], pt[1], 0]
1469
1470        # NB: every time the mesh moves or is warped the locators are set to None
1471        if ((n > 1 or radius) or (n == 1 and return_point_id)) and not return_cell_id:
1472            poly = None
1473            if not self.point_locator:
1474                poly = self.dataset
1475                self.point_locator = vtki.new("StaticPointLocator")
1476                self.point_locator.SetDataSet(poly)
1477                self.point_locator.BuildLocator()
1478
1479            ##########
1480            if radius:
1481                vtklist = vtki.vtkIdList()
1482                self.point_locator.FindPointsWithinRadius(radius, pt, vtklist)
1483            elif n > 1:
1484                vtklist = vtki.vtkIdList()
1485                self.point_locator.FindClosestNPoints(n, pt, vtklist)
1486            else:  # n==1 hence return_point_id==True
1487                ########
1488                return self.point_locator.FindClosestPoint(pt)
1489                ########
1490
1491            if return_point_id:
1492                ########
1493                return utils.vtk2numpy(vtklist)
1494                ########
1495
1496            if not poly:
1497                poly = self.dataset
1498            trgp = []
1499            for i in range(vtklist.GetNumberOfIds()):
1500                trgp_ = [0, 0, 0]
1501                vi = vtklist.GetId(i)
1502                poly.GetPoints().GetPoint(vi, trgp_)
1503                trgp.append(trgp_)
1504            ########
1505            return np.array(trgp)
1506            ########
1507
1508        else:
1509
1510            if not self.cell_locator:
1511                poly = self.dataset
1512
1513                # As per Miquel example with limbs the vtkStaticCellLocator doesnt work !!
1514                # https://discourse.vtk.org/t/vtkstaticcelllocator-problem-vtk9-0-3/7854/4
1515                if vedo.vtk_version[0] >= 9 and vedo.vtk_version[1] > 0:
1516                    self.cell_locator = vtki.new("StaticCellLocator")
1517                else:
1518                    self.cell_locator = vtki.new("CellLocator")
1519
1520                self.cell_locator.SetDataSet(poly)
1521                self.cell_locator.BuildLocator()
1522
1523            if radius is not None:
1524                vedo.printc("Warning: closest_point() with radius is not implemented for cells.", c='r')
1525
1526            if n != 1:
1527                vedo.printc("Warning: closest_point() with n>1 is not implemented for cells.", c='r')
1528
1529            trgp = [0, 0, 0]
1530            cid = vtki.mutable(0)
1531            dist2 = vtki.mutable(0)
1532            subid = vtki.mutable(0)
1533            self.cell_locator.FindClosestPoint(pt, trgp, cid, subid, dist2)
1534
1535            if return_cell_id:
1536                return int(cid)
1537
1538            return np.array(trgp)
1539
1540    def auto_distance(self) -> np.ndarray:
1541        """
1542        Calculate the distance to the closest point in the same cloud of points.
1543        The output is stored in a new pointdata array called "AutoDistance",
1544        and it is also returned by the function.
1545        """
1546        points = self.coordinates
1547        if not self.point_locator:
1548            self.point_locator = vtki.new("StaticPointLocator")
1549            self.point_locator.SetDataSet(self.dataset)
1550            self.point_locator.BuildLocator()
1551        qs = []
1552        vtklist = vtki.vtkIdList()
1553        vtkpoints = self.dataset.GetPoints()
1554        for p in points:
1555            self.point_locator.FindClosestNPoints(2, p, vtklist)
1556            q = [0, 0, 0]
1557            pid = vtklist.GetId(1)
1558            vtkpoints.GetPoint(pid, q)
1559            qs.append(q)
1560        dists = np.linalg.norm(points - np.array(qs), axis=1)
1561        self.pointdata["AutoDistance"] = dists
1562        return dists
1563
1564    def hausdorff_distance(self, points) -> float:
1565        """
1566        Compute the Hausdorff distance to the input point set.
1567        Returns a single `float`.
1568
1569        Example:
1570            ```python
1571            from vedo import *
1572            t = np.linspace(0, 2*np.pi, 100)
1573            x = 4/3 * sin(t)**3
1574            y = cos(t) - cos(2*t)/3 - cos(3*t)/6 - cos(4*t)/12
1575            pol1 = Line(np.c_[x,y], closed=True).triangulate()
1576            pol2 = Polygon(nsides=5).pos(2,2)
1577            d12 = pol1.distance_to(pol2)
1578            d21 = pol2.distance_to(pol1)
1579            pol1.lw(0).cmap("viridis")
1580            pol2.lw(0).cmap("viridis")
1581            print("distance d12, d21 :", min(d12), min(d21))
1582            print("hausdorff distance:", pol1.hausdorff_distance(pol2))
1583            print("chamfer distance  :", pol1.chamfer_distance(pol2))
1584            show(pol1, pol2, axes=1)
1585            ```
1586 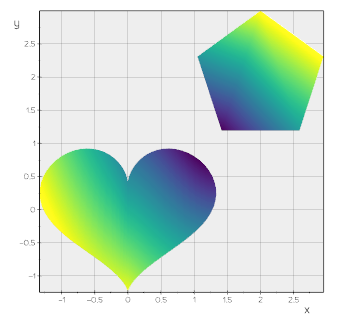           ![](https://vedo.embl.es/images/feats/heart.png)
1587        """
1588        hp = vtki.new("HausdorffDistancePointSetFilter")
1589        hp.SetInputData(0, self.dataset)
1590        hp.SetInputData(1, points.dataset)
1591        hp.SetTargetDistanceMethodToPointToCell()
1592        hp.Update()
1593        return hp.GetHausdorffDistance()
1594
1595    def chamfer_distance(self, pcloud) -> float:
1596        """
1597        Compute the Chamfer distance to the input point set.
1598
1599        Example:
1600            ```python
1601            from vedo import *
1602            cloud1 = np.random.randn(1000, 3)
1603            cloud2 = np.random.randn(1000, 3) + [1, 2, 3]
1604            c1 = Points(cloud1, r=5, c="red")
1605            c2 = Points(cloud2, r=5, c="green")
1606            d = c1.chamfer_distance(c2)
1607            show(f"Chamfer distance = {d}", c1, c2, axes=1).close()
1608            ```
1609        """
1610        # Definition of Chamfer distance may vary, here we use the average
1611        if not pcloud.point_locator:
1612            pcloud.point_locator = vtki.new("PointLocator")
1613            pcloud.point_locator.SetDataSet(pcloud.dataset)
1614            pcloud.point_locator.BuildLocator()
1615        if not self.point_locator:
1616            self.point_locator = vtki.new("PointLocator")
1617            self.point_locator.SetDataSet(self.dataset)
1618            self.point_locator.BuildLocator()
1619
1620        ps1 = self.coordinates
1621        ps2 = pcloud.coordinates
1622
1623        ids12 = []
1624        for p in ps1:
1625            pid12 = pcloud.point_locator.FindClosestPoint(p)
1626            ids12.append(pid12)
1627        deltav = ps2[ids12] - ps1
1628        da = np.mean(np.linalg.norm(deltav, axis=1))
1629
1630        ids21 = []
1631        for p in ps2:
1632            pid21 = self.point_locator.FindClosestPoint(p)
1633            ids21.append(pid21)
1634        deltav = ps1[ids21] - ps2
1635        db = np.mean(np.linalg.norm(deltav, axis=1))
1636        return (da + db) / 2
1637
1638    def remove_outliers(self, radius: float, neighbors=5) -> Self:
1639        """
1640        Remove outliers from a cloud of points within the specified `radius` search.
1641
1642        Arguments:
1643            radius : (float)
1644                Specify the local search radius.
1645            neighbors : (int)
1646                Specify the number of neighbors that a point must have,
1647                within the specified radius, for the point to not be considered isolated.
1648
1649        Examples:
1650            - [clustering.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/clustering.py)
1651
1652 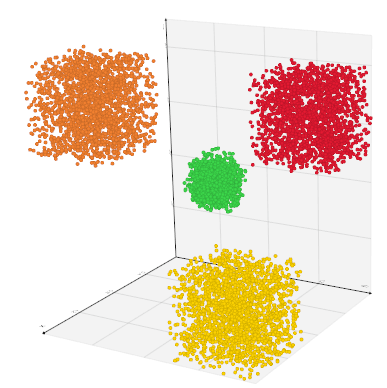               ![](https://vedo.embl.es/images/basic/clustering.png)
1653        """
1654        removal = vtki.new("RadiusOutlierRemoval")
1655        removal.SetInputData(self.dataset)
1656        removal.SetRadius(radius)
1657        removal.SetNumberOfNeighbors(neighbors)
1658        removal.GenerateOutliersOff()
1659        removal.Update()
1660        inputobj = removal.GetOutput()
1661        if inputobj.GetNumberOfCells() == 0:
1662            carr = vtki.vtkCellArray()
1663            for i in range(inputobj.GetNumberOfPoints()):
1664                carr.InsertNextCell(1)
1665                carr.InsertCellPoint(i)
1666            inputobj.SetVerts(carr)
1667        self._update(removal.GetOutput())
1668        self.pipeline = utils.OperationNode("remove_outliers", parents=[self])
1669        return self
1670
1671    def relax_point_positions(
1672            self,
1673            n=10,
1674            iters=10,
1675            sub_iters=10,
1676            packing_factor=1,
1677            max_step=0,
1678            constraints=(),
1679        ) -> Self:
1680        """
1681        Smooth mesh or points with a
1682        [Laplacian algorithm](https://vtk.org/doc/nightly/html/classvtkPointSmoothingFilter.html)
1683        variant. This modifies the coordinates of the input points by adjusting their positions
1684        to create a smooth distribution (and thereby form a pleasing packing of the points).
1685        Smoothing is performed by considering the effects of neighboring points on one another
1686        it uses a cubic cutoff function to produce repulsive forces between close points
1687        and attractive forces that are a little further away.
1688
1689        In general, the larger the neighborhood size, the greater the reduction in high frequency
1690        information. The memory and computational requirements of the algorithm may also
1691        significantly increase.
1692
1693        The algorithm incrementally adjusts the point positions through an iterative process.
1694        Basically points are moved due to the influence of neighboring points.
1695
1696        As points move, both the local connectivity and data attributes associated with each point
1697        must be updated. Rather than performing these expensive operations after every iteration,
1698        a number of sub-iterations can be specified. If so, then the neighborhood and attribute
1699        value updates occur only every sub iteration, which can improve performance significantly.
1700
1701        Arguments:
1702            n : (int)
1703                neighborhood size to calculate the Laplacian.
1704            iters : (int)
1705                number of iterations.
1706            sub_iters : (int)
1707                number of sub-iterations, i.e. the number of times the neighborhood and attribute
1708                value updates occur during each iteration.
1709            packing_factor : (float)
1710                adjust convergence speed.
1711            max_step : (float)
1712                Specify the maximum smoothing step size for each smoothing iteration.
1713                This limits the the distance over which a point can move in each iteration.
1714                As in all iterative methods, the stability of the process is sensitive to this parameter.
1715                In general, small step size and large numbers of iterations are more stable than a larger
1716                step size and a smaller numbers of iterations.
1717            constraints : (dict)
1718                dictionary of constraints.
1719                Point constraints are used to prevent points from moving,
1720                or to move only on a plane. This can prevent shrinking or growing point clouds.
1721                If enabled, a local topological analysis is performed to determine whether a point
1722                should be marked as fixed" i.e., never moves, or the point only moves on a plane,
1723                or the point can move freely.
1724                If all points in the neighborhood surrounding a point are in the cone defined by
1725                `fixed_angle`, then the point is classified as fixed.
1726                If all points in the neighborhood surrounding a point are in the cone defined by
1727                `boundary_angle`, then the point is classified as lying on a plane.
1728                Angles are expressed in degrees.
1729
1730        Example:
1731            ```py
1732            import numpy as np
1733            from vedo import Points, show
1734            from vedo.pyplot import histogram
1735
1736            vpts1 = Points(np.random.rand(10_000, 3))
1737            dists = vpts1.auto_distance()
1738            h1 = histogram(dists, xlim=(0,0.08)).clone2d()
1739
1740            vpts2 = vpts1.clone().relax_point_positions(n=100, iters=20, sub_iters=10)
1741            dists = vpts2.auto_distance()
1742            h2 = histogram(dists, xlim=(0,0.08)).clone2d()
1743
1744            show([[vpts1, h1], [vpts2, h2]], N=2).close()
1745            ```
1746        """
1747        smooth = vtki.new("PointSmoothingFilter")
1748        smooth.SetInputData(self.dataset)
1749        smooth.SetSmoothingModeToUniform()
1750        smooth.SetNumberOfIterations(iters)
1751        smooth.SetNumberOfSubIterations(sub_iters)
1752        smooth.SetPackingFactor(packing_factor)
1753        if self.point_locator:
1754            smooth.SetLocator(self.point_locator)
1755        if not max_step:
1756            max_step = self.diagonal_size() / 100
1757        smooth.SetMaximumStepSize(max_step)
1758        smooth.SetNeighborhoodSize(n)
1759        if constraints:
1760            fixed_angle = constraints.get("fixed_angle", 45)
1761            boundary_angle = constraints.get("boundary_angle", 110)
1762            smooth.EnableConstraintsOn()
1763            smooth.SetFixedAngle(fixed_angle)
1764            smooth.SetBoundaryAngle(boundary_angle)
1765            smooth.GenerateConstraintScalarsOn()
1766            smooth.GenerateConstraintNormalsOn()
1767        smooth.Update()
1768        self._update(smooth.GetOutput())
1769        self.metadata["PackingRadius"] = smooth.GetPackingRadius()
1770        self.pipeline = utils.OperationNode("relax_point_positions", parents=[self])
1771        return self
1772
1773    def smooth_mls_1d(self, f=0.2, radius=None, n=0) -> Self:
1774        """
1775        Smooth mesh or points with a `Moving Least Squares` variant.
1776        The point data array "Variances" will contain the residue calculated for each point.
1777
1778        Arguments:
1779            f : (float)
1780                smoothing factor - typical range is [0,2].
1781            radius : (float)
1782                radius search in absolute units.
1783                If set then `f` is ignored.
1784            n : (int)
1785                number of neighbours to be used for the fit.
1786                If set then `f` and `radius` are ignored.
1787
1788        Examples:
1789            - [moving_least_squares1D.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/moving_least_squares1D.py)
1790            - [skeletonize.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/skeletonize.py)
1791
1792            ![](https://vedo.embl.es/images/advanced/moving_least_squares1D.png)
1793        """
1794        coords = self.coordinates
1795        ncoords = len(coords)
1796
1797        if n:
1798            Ncp = n
1799        elif radius:
1800            Ncp = 1
1801        else:
1802            Ncp = int(ncoords * f / 10)
1803            if Ncp < 5:
1804                vedo.logger.warning(f"Please choose a fraction higher than {f}")
1805                Ncp = 5
1806
1807        variances, newline = [], []
1808        for p in coords:
1809            points = self.closest_point(p, n=Ncp, radius=radius)
1810            if len(points) < 4:
1811                continue
1812
1813            points = np.array(points)
1814            pointsmean = points.mean(axis=0)  # plane center
1815            _, dd, vv = np.linalg.svd(points - pointsmean)
1816            newp = np.dot(p - pointsmean, vv[0]) * vv[0] + pointsmean
1817            variances.append(dd[1] + dd[2])
1818            newline.append(newp)
1819
1820        self.pointdata["Variances"] = np.array(variances).astype(np.float32)
1821        self.coordinates = newline
1822        self.pipeline = utils.OperationNode("smooth_mls_1d", parents=[self])
1823        return self
1824
1825    def smooth_mls_2d(self, f=0.2, radius=None, n=0) -> Self:
1826        """
1827        Smooth mesh or points with a `Moving Least Squares` algorithm variant.
1828
1829        The `mesh.pointdata['MLSVariance']` array will contain the residue calculated for each point.
1830        When a radius is specified, points that are isolated will not be moved and will get
1831        a 0 entry in array `mesh.pointdata['MLSValidPoint']`.
1832
1833        Arguments:
1834            f : (float)
1835                smoothing factor - typical range is [0, 2].
1836            radius : (float | array)
1837                radius search in absolute units. Can be single value (float) or sequence
1838                for adaptive smoothing. If set then `f` is ignored.
1839            n : (int)
1840                number of neighbours to be used for the fit.
1841                If set then `f` and `radius` are ignored.
1842
1843        Examples:
1844            - [moving_least_squares2D.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/moving_least_squares2D.py)
1845            - [recosurface.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/recosurface.py)
1846
1847                ![](https://vedo.embl.es/images/advanced/recosurface.png)
1848        """
1849        coords = self.coordinates
1850        ncoords = len(coords)
1851
1852        if n:
1853            Ncp = n
1854            radius = None
1855        elif radius is not None:
1856            Ncp = 1
1857        else:
1858            Ncp = int(ncoords * f / 100)
1859            if Ncp < 4:
1860                vedo.logger.error(f"please choose a f-value higher than {f}")
1861                Ncp = 4
1862
1863        variances, newpts, valid = [], [], []
1864        radius_is_sequence = utils.is_sequence(radius)
1865
1866        pb = None
1867        if ncoords > 10000:
1868            pb = utils.ProgressBar(0, ncoords, delay=3)
1869
1870        for i, p in enumerate(coords):
1871            if pb:
1872                pb.print("smooth_mls_2d working ...")
1873
1874            # if a radius was provided for each point
1875            if radius_is_sequence:
1876                pts = self.closest_point(p, n=Ncp, radius=radius[i])
1877            else:
1878                pts = self.closest_point(p, n=Ncp, radius=radius)
1879
1880            if len(pts) > 3:
1881                ptsmean = pts.mean(axis=0)  # plane center
1882                _, dd, vv = np.linalg.svd(pts - ptsmean)
1883                cv = np.cross(vv[0], vv[1])
1884                t = (np.dot(cv, ptsmean) - np.dot(cv, p)) / np.dot(cv, cv)
1885                newpts.append(p + cv * t)
1886                variances.append(dd[2])
1887                if radius is not None:
1888                    valid.append(1)
1889            else:
1890                newpts.append(p)
1891                variances.append(0)
1892                if radius is not None:
1893                    valid.append(0)
1894
1895        if radius is not None:
1896            self.pointdata["MLSValidPoint"] = np.array(valid).astype(np.uint8)
1897        self.pointdata["MLSVariance"] = np.array(variances).astype(np.float32)
1898
1899        self.coordinates = newpts
1900
1901        self.pipeline = utils.OperationNode("smooth_mls_2d", parents=[self])
1902        return self
1903
1904    def smooth_lloyd_2d(self, iterations=2, bounds=None, options="Qbb Qc Qx") -> Self:
1905        """
1906        Lloyd relaxation of a 2D pointcloud.
1907
1908        Arguments:
1909            iterations : (int)
1910                number of iterations.
1911            bounds : (list)
1912                bounding box of the domain.
1913            options : (str)
1914                options for the Qhull algorithm.
1915        """
1916        # Credits: https://hatarilabs.com/ih-en/
1917        # tutorial-to-create-a-geospatial-voronoi-sh-mesh-with-python-scipy-and-geopandas
1918        from scipy.spatial import Voronoi as scipy_voronoi
1919
1920        def _constrain_points(points):
1921            # Update any points that have drifted beyond the boundaries of this space
1922            if bounds is not None:
1923                for point in points:
1924                    if point[0] < bounds[0]: point[0] = bounds[0]
1925                    if point[0] > bounds[1]: point[0] = bounds[1]
1926                    if point[1] < bounds[2]: point[1] = bounds[2]
1927                    if point[1] > bounds[3]: point[1] = bounds[3]
1928            return points
1929
1930        def _find_centroid(vertices):
1931            # The equation for the method used here to find the centroid of a
1932            # 2D polygon is given here: https://en.wikipedia.org/wiki/Centroid#Of_a_polygon
1933            area = 0
1934            centroid_x = 0
1935            centroid_y = 0
1936            for i in range(len(vertices) - 1):
1937                step = (vertices[i, 0] * vertices[i + 1, 1]) - (vertices[i + 1, 0] * vertices[i, 1])
1938                centroid_x += (vertices[i, 0] + vertices[i + 1, 0]) * step
1939                centroid_y += (vertices[i, 1] + vertices[i + 1, 1]) * step
1940                area += step
1941            if area:
1942                centroid_x = (1.0 / (3.0 * area)) * centroid_x
1943                centroid_y = (1.0 / (3.0 * area)) * centroid_y
1944            # prevent centroids from escaping bounding box
1945            return _constrain_points([[centroid_x, centroid_y]])[0]
1946
1947        def _relax(voron):
1948            # Moves each point to the centroid of its cell in the voronoi
1949            # map to "relax" the points (i.e. jitter the points so as
1950            # to spread them out within the space).
1951            centroids = []
1952            for idx in voron.point_region:
1953                # the region is a series of indices into voronoi.vertices
1954                # remove point at infinity, designated by index -1
1955                region = [i for i in voron.regions[idx] if i != -1]
1956                # enclose the polygon
1957                region = region + [region[0]]
1958                verts = voron.vertices[region]
1959                # find the centroid of those vertices
1960                centroids.append(_find_centroid(verts))
1961            return _constrain_points(centroids)
1962
1963        if bounds is None:
1964            bounds = self.bounds()
1965
1966        pts = self.vertices[:, (0, 1)]
1967        for i in range(iterations):
1968            vor = scipy_voronoi(pts, qhull_options=options)
1969            _constrain_points(vor.vertices)
1970            pts = _relax(vor)
1971        out = Points(pts)
1972        out.name = "MeshSmoothLloyd2D"
1973        out.pipeline = utils.OperationNode("smooth_lloyd", parents=[self])
1974        return out
1975
1976    def project_on_plane(self, plane="z", point=None, direction=None) -> Self:
1977        """
1978        Project the mesh on one of the Cartesian planes.
1979
1980        Arguments:
1981            plane : (str, Plane)
1982                if plane is `str`, plane can be one of ['x', 'y', 'z'],
1983                represents x-plane, y-plane and z-plane, respectively.
1984                Otherwise, plane should be an instance of `vedo.shapes.Plane`.
1985            point : (float, array)
1986                if plane is `str`, point should be a float represents the intercept.
1987                Otherwise, point is the camera point of perspective projection
1988            direction : (array)
1989                direction of oblique projection
1990
1991        Note:
1992            Parameters `point` and `direction` are only used if the given plane
1993            is an instance of `vedo.shapes.Plane`. And one of these two params
1994            should be left as `None` to specify the projection type.
1995
1996        Example:
1997            ```python
1998            s.project_on_plane(plane='z') # project to z-plane
1999            plane = Plane(pos=(4, 8, -4), normal=(-1, 0, 1), s=(5,5))
2000            s.project_on_plane(plane=plane)                       # orthogonal projection
2001            s.project_on_plane(plane=plane, point=(6, 6, 6))      # perspective projection
2002            s.project_on_plane(plane=plane, direction=(1, 2, -1)) # oblique projection
2003            ```
2004
2005        Examples:
2006            - [silhouette2.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/silhouette2.py)
2007
2008 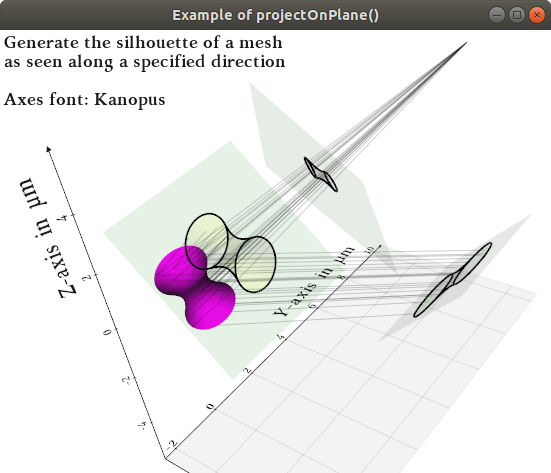               ![](https://vedo.embl.es/images/basic/silhouette2.png)
2009        """
2010        coords = self.coordinates
2011
2012        if plane == "x":
2013            coords[:, 0] = self.transform.position[0]
2014            intercept = self.xbounds()[0] if point is None else point
2015            self.x(intercept)
2016        elif plane == "y":
2017            coords[:, 1] = self.transform.position[1]
2018            intercept = self.ybounds()[0] if point is None else point
2019            self.y(intercept)
2020        elif plane == "z":
2021            coords[:, 2] = self.transform.position[2]
2022            intercept = self.zbounds()[0] if point is None else point
2023            self.z(intercept)
2024
2025        elif isinstance(plane, vedo.shapes.Plane):
2026            normal = plane.normal / np.linalg.norm(plane.normal)
2027            pl = np.hstack((normal, -np.dot(plane.pos(), normal))).reshape(4, 1)
2028            if direction is None and point is None:
2029                # orthogonal projection
2030                pt = np.hstack((normal, [0])).reshape(4, 1)
2031                # proj_mat = pt.T @ pl * np.eye(4) - pt @ pl.T # python3 only
2032                proj_mat = np.matmul(pt.T, pl) * np.eye(4) - np.matmul(pt, pl.T)
2033
2034            elif direction is None:
2035                # perspective projection
2036                pt = np.hstack((np.array(point), [1])).reshape(4, 1)
2037                # proj_mat = pt.T @ pl * np.eye(4) - pt @ pl.T
2038                proj_mat = np.matmul(pt.T, pl) * np.eye(4) - np.matmul(pt, pl.T)
2039
2040            elif point is None:
2041                # oblique projection
2042                pt = np.hstack((np.array(direction), [0])).reshape(4, 1)
2043                # proj_mat = pt.T @ pl * np.eye(4) - pt @ pl.T
2044                proj_mat = np.matmul(pt.T, pl) * np.eye(4) - np.matmul(pt, pl.T)
2045
2046            coords = np.concatenate([coords, np.ones((coords.shape[:-1] + (1,)))], axis=-1)
2047            # coords = coords @ proj_mat.T
2048            coords = np.matmul(coords, proj_mat.T)
2049            coords = coords[:, :3] / coords[:, 3:]
2050
2051        else:
2052            vedo.logger.error(f"unknown plane {plane}")
2053            raise RuntimeError()
2054
2055        self.alpha(0.1)
2056        self.coordinates = coords
2057        return self
2058
2059    def warp(self, source, target, sigma=1.0, mode="3d") -> Self:
2060        """
2061        "Thin Plate Spline" transformations describe a nonlinear warp transform defined by a set
2062        of source and target landmarks. Any point on the mesh close to a source landmark will
2063        be moved to a place close to the corresponding target landmark.
2064        The points in between are interpolated smoothly using
2065        Bookstein's Thin Plate Spline algorithm.
2066
2067        Transformation object can be accessed with `mesh.transform`.
2068
2069        Arguments:
2070            sigma : (float)
2071                specify the 'stiffness' of the spline.
2072            mode : (str)
2073                set the basis function to either abs(R) (for 3d) or R2LogR (for 2d meshes)
2074
2075        Examples:
2076            - [interpolate_field.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/interpolate_field.py)
2077            - [warp1.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/warp1.py)
2078            - [warp2.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/warp2.py)
2079            - [warp3.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/warp3.py)
2080            - [warp4a.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/warp4a.py)
2081            - [warp4b.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/warp4b.py)
2082            - [warp6.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/warp6.py)
2083
2084 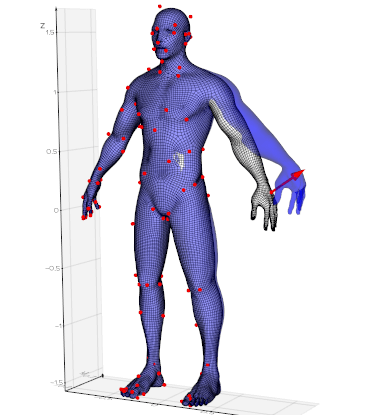           ![](https://vedo.embl.es/images/advanced/warp2.png)
2085        """
2086        parents = [self]
2087
2088        try:
2089            source = source.coordinates
2090            parents.append(source)
2091        except AttributeError:
2092            source = utils.make3d(source)
2093
2094        try:
2095            target = target.coordinates
2096            parents.append(target)
2097        except AttributeError:
2098            target = utils.make3d(target)
2099
2100        ns = len(source)
2101        nt = len(target)
2102        if ns != nt:
2103            vedo.logger.error(f"#source {ns} != {nt} #target points")
2104            raise RuntimeError()
2105
2106        NLT = NonLinearTransform(sigma=sigma, mode=mode)
2107        NLT.source_points = source
2108        NLT.target_points = target
2109        self.apply_transform(NLT)
2110
2111        self.pipeline = utils.OperationNode("warp", parents=parents)
2112        return self
2113
2114    def cut_with_plane(
2115            self,
2116            origin=(0, 0, 0),
2117            normal=(1, 0, 0),
2118            invert=False,
2119            # generate_ids=False,
2120    ) -> Self:
2121        """
2122        Cut the mesh with the plane defined by a point and a normal.
2123
2124        Arguments:
2125            origin : (array)
2126                the cutting plane goes through this point
2127            normal : (array)
2128                normal of the cutting plane
2129            invert : (bool)
2130                select which side of the plane to keep
2131
2132        Example:
2133            ```python
2134            from vedo import Cube
2135            cube = Cube().cut_with_plane(normal=(1,1,1))
2136            cube.back_color('pink').show().close()
2137            ```
2138 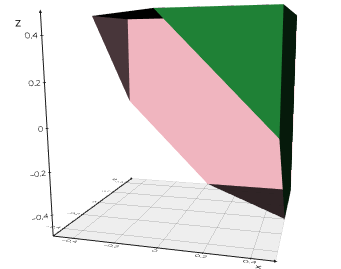           ![](https://vedo.embl.es/images/feats/cut_with_plane_cube.png)
2139
2140        Examples:
2141            - [trail.py](https://github.com/marcomusy/vedo/blob/master/examples/simulations/trail.py)
2142
2143                ![](https://vedo.embl.es/images/simulations/trail.gif)
2144
2145        Check out also:
2146            `cut_with_box()`, `cut_with_cylinder()`, `cut_with_sphere()`.
2147        """
2148        s = str(normal)
2149        if "x" in s:
2150            normal = (1, 0, 0)
2151            if "-" in s:
2152                normal = -np.array(normal)
2153        elif "y" in s:
2154            normal = (0, 1, 0)
2155            if "-" in s:
2156                normal = -np.array(normal)
2157        elif "z" in s:
2158            normal = (0, 0, 1)
2159            if "-" in s:
2160                normal = -np.array(normal)
2161        plane = vtki.vtkPlane()
2162        plane.SetOrigin(origin)
2163        plane.SetNormal(normal)
2164
2165        clipper = vtki.new("ClipPolyData")
2166        clipper.SetInputData(self.dataset)
2167        clipper.SetClipFunction(plane)
2168        clipper.GenerateClippedOutputOff()
2169        clipper.SetGenerateClipScalars(0)
2170        clipper.SetInsideOut(invert)
2171        clipper.SetValue(0)
2172        clipper.Update()
2173
2174        # if generate_ids:
2175        #     saved_scalars = None # otherwise the scalars are lost
2176        #     if self.dataset.GetPointData().GetScalars():
2177        #         saved_scalars = self.dataset.GetPointData().GetScalars()
2178        #     varr = clipper.GetOutput().GetPointData().GetScalars()
2179        #     if varr.GetName() is None:
2180        #         varr.SetName("DistanceToCut")
2181        #     arr = utils.vtk2numpy(varr)
2182        #     # array of original ids
2183        #     ids = np.arange(arr.shape[0]).astype(int)
2184        #     ids[arr == 0] = -1
2185        #     ids_arr = utils.numpy2vtk(ids, dtype=int)
2186        #     ids_arr.SetName("OriginalIds")
2187        #     clipper.GetOutput().GetPointData().AddArray(ids_arr)
2188        #     if saved_scalars:
2189        #         clipper.GetOutput().GetPointData().AddArray(saved_scalars)
2190
2191        self._update(clipper.GetOutput())
2192        self.pipeline = utils.OperationNode("cut_with_plane", parents=[self])
2193        return self
2194
2195    def cut_with_planes(self, origins, normals, invert=False) -> Self:
2196        """
2197        Cut the mesh with a convex set of planes defined by points and normals.
2198
2199        Arguments:
2200            origins : (array)
2201                each cutting plane goes through this point
2202            normals : (array)
2203                normal of each of the cutting planes
2204            invert : (bool)
2205                if True, cut outside instead of inside
2206
2207        Check out also:
2208            `cut_with_box()`, `cut_with_cylinder()`, `cut_with_sphere()`
2209        """
2210
2211        vpoints = vtki.vtkPoints()
2212        for p in utils.make3d(origins):
2213            vpoints.InsertNextPoint(p)
2214        normals = utils.make3d(normals)
2215
2216        planes = vtki.vtkPlanes()
2217        planes.SetPoints(vpoints)
2218        planes.SetNormals(utils.numpy2vtk(normals, dtype=float))
2219
2220        clipper = vtki.new("ClipPolyData")
2221        clipper.SetInputData(self.dataset)
2222        clipper.SetInsideOut(invert)
2223        clipper.SetClipFunction(planes)
2224        clipper.GenerateClippedOutputOff()
2225        clipper.GenerateClipScalarsOff()
2226        clipper.SetValue(0)
2227        clipper.Update()
2228
2229        self._update(clipper.GetOutput())
2230
2231        self.pipeline = utils.OperationNode("cut_with_planes", parents=[self])
2232        return self
2233
2234    def cut_with_box(self, bounds, invert=False) -> Self:
2235        """
2236        Cut the current mesh with a box or a set of boxes.
2237        This is much faster than `cut_with_mesh()`.
2238
2239        Input `bounds` can be either:
2240        - a Mesh or Points object
2241        - a list of 6 number representing a bounding box `[xmin,xmax, ymin,ymax, zmin,zmax]`
2242        - a list of bounding boxes like the above: `[[xmin1,...], [xmin2,...], ...]`
2243
2244        Example:
2245            ```python
2246            from vedo import Sphere, Cube, show
2247            mesh = Sphere(r=1, res=50)
2248            box  = Cube(side=1.5).wireframe()
2249            mesh.cut_with_box(box)
2250            show(mesh, box, axes=1).close()
2251            ```
2252            ![](https://vedo.embl.es/images/feats/cut_with_box_cube.png)
2253
2254        Check out also:
2255            `cut_with_line()`, `cut_with_plane()`, `cut_with_cylinder()`
2256        """
2257        if isinstance(bounds, Points):
2258            bounds = bounds.bounds()
2259
2260        box = vtki.new("Box")
2261        if utils.is_sequence(bounds[0]):
2262            for bs in bounds:
2263                box.AddBounds(bs)
2264        else:
2265            box.SetBounds(bounds)
2266
2267        clipper = vtki.new("ClipPolyData")
2268        clipper.SetInputData(self.dataset)
2269        clipper.SetClipFunction(box)
2270        clipper.SetInsideOut(not invert)
2271        clipper.GenerateClippedOutputOff()
2272        clipper.GenerateClipScalarsOff()
2273        clipper.SetValue(0)
2274        clipper.Update()
2275        self._update(clipper.GetOutput())
2276
2277        self.pipeline = utils.OperationNode("cut_with_box", parents=[self])
2278        return self
2279
2280    def cut_with_line(self, points, invert=False, closed=True) -> Self:
2281        """
2282        Cut the current mesh with a line vertically in the z-axis direction like a cookie cutter.
2283        The polyline is defined by a set of points (z-coordinates are ignored).
2284        This is much faster than `cut_with_mesh()`.
2285
2286        Check out also:
2287            `cut_with_box()`, `cut_with_plane()`, `cut_with_sphere()`
2288        """
2289        pplane = vtki.new("PolyPlane")
2290        if isinstance(points, Points):
2291            points = points.coordinates.tolist()
2292
2293        if closed:
2294            if isinstance(points, np.ndarray):
2295                points = points.tolist()
2296            points.append(points[0])
2297
2298        vpoints = vtki.vtkPoints()
2299        for p in points:
2300            if len(p) == 2:
2301                p = [p[0], p[1], 0.0]
2302            vpoints.InsertNextPoint(p)
2303
2304        n = len(points)
2305        polyline = vtki.new("PolyLine")
2306        polyline.Initialize(n, vpoints)
2307        polyline.GetPointIds().SetNumberOfIds(n)
2308        for i in range(n):
2309            polyline.GetPointIds().SetId(i, i)
2310        pplane.SetPolyLine(polyline)
2311
2312        clipper = vtki.new("ClipPolyData")
2313        clipper.SetInputData(self.dataset)
2314        clipper.SetClipFunction(pplane)
2315        clipper.SetInsideOut(invert)
2316        clipper.GenerateClippedOutputOff()
2317        clipper.GenerateClipScalarsOff()
2318        clipper.SetValue(0)
2319        clipper.Update()
2320        self._update(clipper.GetOutput())
2321
2322        self.pipeline = utils.OperationNode("cut_with_line", parents=[self])
2323        return self
2324
2325    def cut_with_cookiecutter(self, lines) -> Self:
2326        """
2327        Cut the current mesh with a single line or a set of lines.
2328
2329        Input `lines` can be either:
2330        - a `Mesh` or `Points` object
2331        - a list of 3D points: `[(x1,y1,z1), (x2,y2,z2), ...]`
2332        - a list of 2D points: `[(x1,y1), (x2,y2), ...]`
2333
2334        Example:
2335            ```python
2336            from vedo import *
2337            grid = Mesh(dataurl + "dolfin_fine.vtk")
2338            grid.compute_quality().cmap("Greens")
2339            pols = merge(
2340                Polygon(nsides=10, r=0.3).pos(0.7, 0.3),
2341                Polygon(nsides=10, r=0.2).pos(0.3, 0.7),
2342            )
2343            lines = pols.boundaries()
2344            cgrid = grid.clone().cut_with_cookiecutter(lines)
2345            grid.alpha(0.1).wireframe()
2346            show(grid, cgrid, lines, axes=8, bg='blackboard').close()
2347            ```
2348 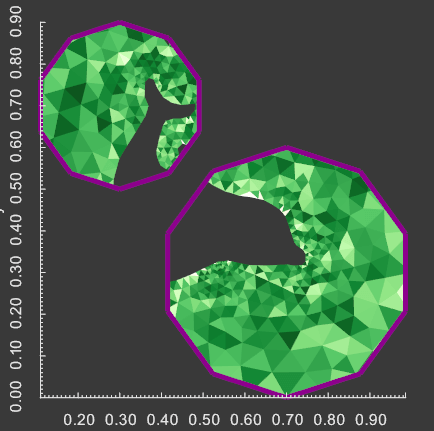           ![](https://vedo.embl.es/images/feats/cookiecutter.png)
2349
2350        Check out also:
2351            `cut_with_line()` and `cut_with_point_loop()`
2352
2353        Note:
2354            In case of a warning message like:
2355                "Mesh and trim loop point data attributes are different"
2356            consider interpolating the mesh point data to the loop points,
2357            Eg. (in the above example):
2358            ```python
2359            lines = pols.boundaries().interpolate_data_from(grid, n=2)
2360            ```
2361
2362        Note:
2363            trying to invert the selection by reversing the loop order
2364            will have no effect in this method, hence it does not have
2365            the `invert` option.
2366        """
2367        if utils.is_sequence(lines):
2368            lines = utils.make3d(lines)
2369            iline = list(range(len(lines))) + [0]
2370            poly = utils.buildPolyData(lines, lines=[iline])
2371        else:
2372            poly = lines.dataset
2373
2374        # if invert: # not working
2375        #     rev = vtki.new("ReverseSense")
2376        #     rev.ReverseCellsOn()
2377        #     rev.SetInputData(poly)
2378        #     rev.Update()
2379        #     poly = rev.GetOutput()
2380
2381        # Build loops from the polyline
2382        build_loops = vtki.new("ContourLoopExtraction")
2383        build_loops.SetGlobalWarningDisplay(0)
2384        build_loops.SetInputData(poly)
2385        build_loops.Update()
2386        boundary_poly = build_loops.GetOutput()
2387
2388        ccut = vtki.new("CookieCutter")
2389        ccut.SetInputData(self.dataset)
2390        ccut.SetLoopsData(boundary_poly)
2391        ccut.SetPointInterpolationToMeshEdges()
2392        # ccut.SetPointInterpolationToLoopEdges()
2393        ccut.PassCellDataOn()
2394        ccut.PassPointDataOn()
2395        ccut.Update()
2396        self._update(ccut.GetOutput())
2397
2398        self.pipeline = utils.OperationNode("cut_with_cookiecutter", parents=[self])
2399        return self
2400
2401    def cut_with_cylinder(self, center=(0, 0, 0), axis=(0, 0, 1), r=1, invert=False) -> Self:
2402        """
2403        Cut the current mesh with an infinite cylinder.
2404        This is much faster than `cut_with_mesh()`.
2405
2406        Arguments:
2407            center : (array)
2408                the center of the cylinder
2409            normal : (array)
2410                direction of the cylinder axis
2411            r : (float)
2412                radius of the cylinder
2413
2414        Example:
2415            ```python
2416            from vedo import Disc, show
2417            disc = Disc(r1=1, r2=1.2)
2418            mesh = disc.extrude(3, res=50).linewidth(1)
2419            mesh.cut_with_cylinder([0,0,2], r=0.4, axis='y', invert=True)
2420            show(mesh, axes=1).close()
2421            ```
2422            ![](https://vedo.embl.es/images/feats/cut_with_cylinder.png)
2423
2424        Examples:
2425            - [optics_main1.py](https://github.com/marcomusy/vedo/blob/master/examples/simulations/optics_main1.py)
2426
2427        Check out also:
2428            `cut_with_box()`, `cut_with_plane()`, `cut_with_sphere()`
2429        """
2430        s = str(axis)
2431        if "x" in s:
2432            axis = (1, 0, 0)
2433        elif "y" in s:
2434            axis = (0, 1, 0)
2435        elif "z" in s:
2436            axis = (0, 0, 1)
2437        cyl = vtki.new("Cylinder")
2438        cyl.SetCenter(center)
2439        cyl.SetAxis(axis[0], axis[1], axis[2])
2440        cyl.SetRadius(r)
2441
2442        clipper = vtki.new("ClipPolyData")
2443        clipper.SetInputData(self.dataset)
2444        clipper.SetClipFunction(cyl)
2445        clipper.SetInsideOut(not invert)
2446        clipper.GenerateClippedOutputOff()
2447        clipper.GenerateClipScalarsOff()
2448        clipper.SetValue(0)
2449        clipper.Update()
2450        self._update(clipper.GetOutput())
2451
2452        self.pipeline = utils.OperationNode("cut_with_cylinder", parents=[self])
2453        return self
2454
2455    def cut_with_sphere(self, center=(0, 0, 0), r=1.0, invert=False) -> Self:
2456        """
2457        Cut the current mesh with an sphere.
2458        This is much faster than `cut_with_mesh()`.
2459
2460        Arguments:
2461            center : (array)
2462                the center of the sphere
2463            r : (float)
2464                radius of the sphere
2465
2466        Example:
2467            ```python
2468            from vedo import Disc, show
2469            disc = Disc(r1=1, r2=1.2)
2470            mesh = disc.extrude(3, res=50).linewidth(1)
2471            mesh.cut_with_sphere([1,-0.7,2], r=1.5, invert=True)
2472            show(mesh, axes=1).close()
2473            ```
2474            ![](https://vedo.embl.es/images/feats/cut_with_sphere.png)
2475
2476        Check out also:
2477            `cut_with_box()`, `cut_with_plane()`, `cut_with_cylinder()`
2478        """
2479        sph = vtki.new("Sphere")
2480        sph.SetCenter(center)
2481        sph.SetRadius(r)
2482
2483        clipper = vtki.new("ClipPolyData")
2484        clipper.SetInputData(self.dataset)
2485        clipper.SetClipFunction(sph)
2486        clipper.SetInsideOut(not invert)
2487        clipper.GenerateClippedOutputOff()
2488        clipper.GenerateClipScalarsOff()
2489        clipper.SetValue(0)
2490        clipper.Update()
2491        self._update(clipper.GetOutput())
2492        self.pipeline = utils.OperationNode("cut_with_sphere", parents=[self])
2493        return self
2494
2495    def cut_with_mesh(self, mesh, invert=False, keep=False) -> Union[Self, "vedo.Assembly"]:
2496        """
2497        Cut an `Mesh` mesh with another `Mesh`.
2498
2499        Use `invert` to invert the selection.
2500
2501        Use `keep` to keep the cutoff part, in this case an `Assembly` is returned:
2502        the "cut" object and the "discarded" part of the original object.
2503        You can access both via `assembly.unpack()` method.
2504
2505        Example:
2506        ```python
2507        from vedo import *
2508        arr = np.random.randn(100000, 3)/2
2509        pts = Points(arr).c('red3').pos(5,0,0)
2510        cube = Cube().pos(4,0.5,0)
2511        assem = pts.cut_with_mesh(cube, keep=True)
2512        show(assem.unpack(), axes=1).close()
2513        ```
2514        ![](https://vedo.embl.es/images/feats/cut_with_mesh.png)
2515
2516       Check out also:
2517            `cut_with_box()`, `cut_with_plane()`, `cut_with_cylinder()`
2518       """
2519        polymesh = mesh.dataset
2520        poly = self.dataset
2521
2522        # Create an array to hold distance information
2523        signed_distances = vtki.vtkFloatArray()
2524        signed_distances.SetNumberOfComponents(1)
2525        signed_distances.SetName("SignedDistances")
2526
2527        # implicit function that will be used to slice the mesh
2528        ippd = vtki.new("ImplicitPolyDataDistance")
2529        ippd.SetInput(polymesh)
2530
2531        # Evaluate the signed distance function at all of the grid points
2532        for pointId in range(poly.GetNumberOfPoints()):
2533            p = poly.GetPoint(pointId)
2534            signed_distance = ippd.EvaluateFunction(p)
2535            signed_distances.InsertNextValue(signed_distance)
2536
2537        currentscals = poly.GetPointData().GetScalars()
2538        if currentscals:
2539            currentscals = currentscals.GetName()
2540
2541        poly.GetPointData().AddArray(signed_distances)
2542        poly.GetPointData().SetActiveScalars("SignedDistances")
2543
2544        clipper = vtki.new("ClipPolyData")
2545        clipper.SetInputData(poly)
2546        clipper.SetInsideOut(not invert)
2547        clipper.SetGenerateClippedOutput(keep)
2548        clipper.SetValue(0.0)
2549        clipper.Update()
2550        cpoly = clipper.GetOutput()
2551
2552        if keep:
2553            kpoly = clipper.GetOutput(1)
2554
2555        vis = False
2556        if currentscals:
2557            cpoly.GetPointData().SetActiveScalars(currentscals)
2558            vis = self.mapper.GetScalarVisibility()
2559
2560        self._update(cpoly)
2561
2562        self.pointdata.remove("SignedDistances")
2563        self.mapper.SetScalarVisibility(vis)
2564        if keep:
2565            if isinstance(self, vedo.Mesh):
2566                cutoff = vedo.Mesh(kpoly)
2567            else:
2568                cutoff = vedo.Points(kpoly)
2569            # cutoff = self.__class__(kpoly) # this does not work properly
2570            cutoff.properties = vtki.vtkProperty()
2571            cutoff.properties.DeepCopy(self.properties)
2572            cutoff.actor.SetProperty(cutoff.properties)
2573            cutoff.c("k5").alpha(0.2)
2574            return vedo.Assembly([self, cutoff])
2575
2576        self.pipeline = utils.OperationNode("cut_with_mesh", parents=[self, mesh])
2577        return self
2578
2579    def cut_with_point_loop(
2580        self, points, invert=False, on="points", include_boundary=False
2581    ) -> Self:
2582        """
2583        Cut an `Mesh` object with a set of points forming a closed loop.
2584
2585        Arguments:
2586            invert : (bool)
2587                invert selection (inside-out)
2588            on : (str)
2589                if 'cells' will extract the whole cells lying inside (or outside) the point loop
2590            include_boundary : (bool)
2591                include cells lying exactly on the boundary line. Only relevant on 'cells' mode
2592
2593        Examples:
2594            - [cut_with_points1.py](https://github.com/marcomusy/vedo/blob/master/examples/advanced/cut_with_points1.py)
2595
2596                ![](https://vedo.embl.es/images/advanced/cutWithPoints1.png)
2597
2598            - [cut_with_points2.py](https://github.com/marcomusy/vedo/blob/master/examples/advanced/cut_with_points2.py)
2599
2600 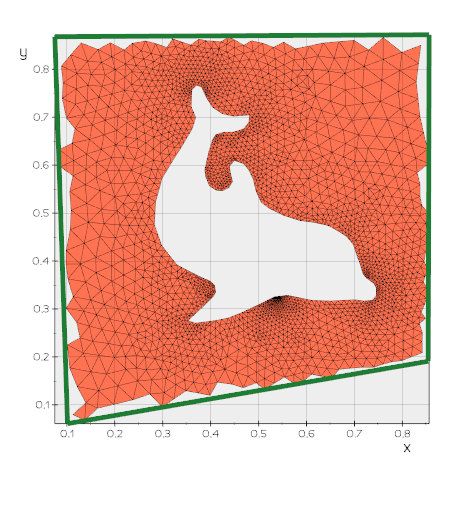               ![](https://vedo.embl.es/images/advanced/cutWithPoints2.png)
2601        """
2602        if isinstance(points, Points):
2603            parents = [points]
2604            vpts = points.dataset.GetPoints()
2605            points = points.coordinates
2606        else:
2607            parents = [self]
2608            vpts = vtki.vtkPoints()
2609            points = utils.make3d(points)
2610            for p in points:
2611                vpts.InsertNextPoint(p)
2612
2613        if "cell" in on:
2614            ippd = vtki.new("ImplicitSelectionLoop")
2615            ippd.SetLoop(vpts)
2616            ippd.AutomaticNormalGenerationOn()
2617            clipper = vtki.new("ExtractPolyDataGeometry")
2618            clipper.SetInputData(self.dataset)
2619            clipper.SetImplicitFunction(ippd)
2620            clipper.SetExtractInside(not invert)
2621            clipper.SetExtractBoundaryCells(include_boundary)
2622        else:
2623            spol = vtki.new("SelectPolyData")
2624            spol.SetLoop(vpts)
2625            spol.GenerateSelectionScalarsOn()
2626            spol.GenerateUnselectedOutputOff()
2627            spol.SetInputData(self.dataset)
2628            spol.Update()
2629            clipper = vtki.new("ClipPolyData")
2630            clipper.SetInputData(spol.GetOutput())
2631            clipper.SetInsideOut(not invert)
2632            clipper.SetValue(0.0)
2633        clipper.Update()
2634        self._update(clipper.GetOutput())
2635
2636        self.pipeline = utils.OperationNode("cut_with_pointloop", parents=parents)
2637        return self
2638
2639    def cut_with_scalar(self, value: float, name="", invert=False) -> Self:
2640        """
2641        Cut a mesh or point cloud with some input scalar point-data.
2642
2643        Arguments:
2644            value : (float)
2645                cutting value
2646            name : (str)
2647                array name of the scalars to be used
2648            invert : (bool)
2649                flip selection
2650
2651        Example:
2652            ```python
2653            from vedo import *
2654            s = Sphere().lw(1)
2655            pts = s.points
2656            scalars = np.sin(3*pts[:,2]) + pts[:,0]
2657            s.pointdata["somevalues"] = scalars
2658            s.cut_with_scalar(0.3)
2659            s.cmap("Spectral", "somevalues").add_scalarbar()
2660            s.show(axes=1).close()
2661            ```
2662            ![](https://vedo.embl.es/images/feats/cut_with_scalars.png)
2663        """
2664        if name:
2665            self.pointdata.select(name)
2666        clipper = vtki.new("ClipPolyData")
2667        clipper.SetInputData(self.dataset)
2668        clipper.SetValue(value)
2669        clipper.GenerateClippedOutputOff()
2670        clipper.SetInsideOut(not invert)
2671        clipper.Update()
2672        self._update(clipper.GetOutput())
2673        self.pipeline = utils.OperationNode("cut_with_scalar", parents=[self])
2674        return self
2675
2676    def crop(self,
2677             top=None, bottom=None, right=None, left=None, front=None, back=None,
2678             bounds=()) -> Self:
2679        """
2680        Crop an `Mesh` object.
2681
2682        Arguments:
2683            top : (float)
2684                fraction to crop from the top plane (positive z)
2685            bottom : (float)
2686                fraction to crop from the bottom plane (negative z)
2687            front : (float)
2688                fraction to crop from the front plane (positive y)
2689            back : (float)
2690                fraction to crop from the back plane (negative y)
2691            right : (float)
2692                fraction to crop from the right plane (positive x)
2693            left : (float)
2694                fraction to crop from the left plane (negative x)
2695            bounds : (list)
2696                bounding box of the crop region as `[x0,x1, y0,y1, z0,z1]`
2697
2698        Example:
2699            ```python
2700            from vedo import Sphere
2701            Sphere().crop(right=0.3, left=0.1).show()
2702            ```
2703 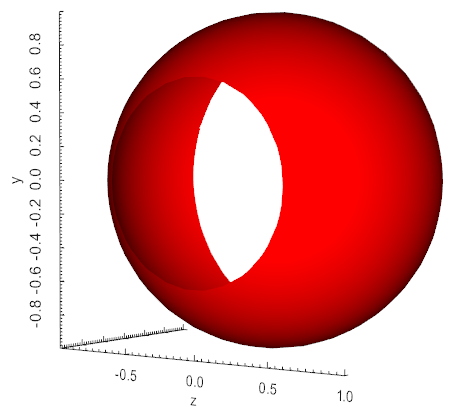           ![](https://user-images.githubusercontent.com/32848391/57081955-0ef1e800-6cf6-11e9-99de-b45220939bc9.png)
2704        """
2705        if len(bounds) == 0:
2706            pos = np.array(self.pos())
2707            x0, x1, y0, y1, z0, z1 = self.bounds()
2708            x0, y0, z0 = [x0, y0, z0] - pos
2709            x1, y1, z1 = [x1, y1, z1] - pos
2710
2711            dx, dy, dz = x1 - x0, y1 - y0, z1 - z0
2712            if top:
2713                z1 = z1 - top * dz
2714            if bottom:
2715                z0 = z0 + bottom * dz
2716            if front:
2717                y1 = y1 - front * dy
2718            if back:
2719                y0 = y0 + back * dy
2720            if right:
2721                x1 = x1 - right * dx
2722            if left:
2723                x0 = x0 + left * dx
2724            bounds = (x0, x1, y0, y1, z0, z1)
2725
2726        cu = vtki.new("Box")
2727        cu.SetBounds(bounds)
2728
2729        clipper = vtki.new("ClipPolyData")
2730        clipper.SetInputData(self.dataset)
2731        clipper.SetClipFunction(cu)
2732        clipper.InsideOutOn()
2733        clipper.GenerateClippedOutputOff()
2734        clipper.GenerateClipScalarsOff()
2735        clipper.SetValue(0)
2736        clipper.Update()
2737        self._update(clipper.GetOutput())
2738
2739        self.pipeline = utils.OperationNode(
2740            "crop", parents=[self], comment=f"#pts {self.dataset.GetNumberOfPoints()}"
2741        )
2742        return self
2743
2744    def generate_surface_halo(
2745            self,
2746            distance=0.05,
2747            res=(50, 50, 50),
2748            bounds=(),
2749            maxdist=None,
2750    ) -> "vedo.Mesh":
2751        """
2752        Generate the surface halo which sits at the specified distance from the input one.
2753
2754        Arguments:
2755            distance : (float)
2756                distance from the input surface
2757            res : (int)
2758                resolution of the surface
2759            bounds : (list)
2760                bounding box of the surface
2761            maxdist : (float)
2762                maximum distance to generate the surface
2763        """
2764        if not bounds:
2765            bounds = self.bounds()
2766
2767        if not maxdist:
2768            maxdist = self.diagonal_size() / 2
2769
2770        imp = vtki.new("ImplicitModeller")
2771        imp.SetInputData(self.dataset)
2772        imp.SetSampleDimensions(res)
2773        if maxdist:
2774            imp.SetMaximumDistance(maxdist)
2775        if len(bounds) == 6:
2776            imp.SetModelBounds(bounds)
2777        contour = vtki.new("ContourFilter")
2778        contour.SetInputConnection(imp.GetOutputPort())
2779        contour.SetValue(0, distance)
2780        contour.Update()
2781        out = vedo.Mesh(contour.GetOutput())
2782        out.c("lightblue").alpha(0.25).lighting("off")
2783        out.pipeline = utils.OperationNode("generate_surface_halo", parents=[self])
2784        return out
2785
2786    def generate_mesh(
2787        self,
2788        line_resolution=None,
2789        mesh_resolution=None,
2790        smooth=0.0,
2791        jitter=0.001,
2792        grid=None,
2793        quads=False,
2794        invert=False,
2795    ) -> Self:
2796        """
2797        Generate a polygonal Mesh from a closed contour line.
2798        If line is not closed it will be closed with a straight segment.
2799
2800        Check also `generate_delaunay2d()`.
2801
2802        Arguments:
2803            line_resolution : (int)
2804                resolution of the contour line. The default is None, in this case
2805                the contour is not resampled.
2806            mesh_resolution : (int)
2807                resolution of the internal triangles not touching the boundary.
2808            smooth : (float)
2809                smoothing of the contour before meshing.
2810            jitter : (float)
2811                add a small noise to the internal points.
2812            grid : (Grid)
2813                manually pass a Grid object. The default is True.
2814            quads : (bool)
2815                generate a mesh of quads instead of triangles.
2816            invert : (bool)
2817                flip the line orientation. The default is False.
2818
2819        Examples:
2820            - [line2mesh_tri.py](https://github.com/marcomusy/vedo/blob/master/examples/advanced/line2mesh_tri.py)
2821
2822 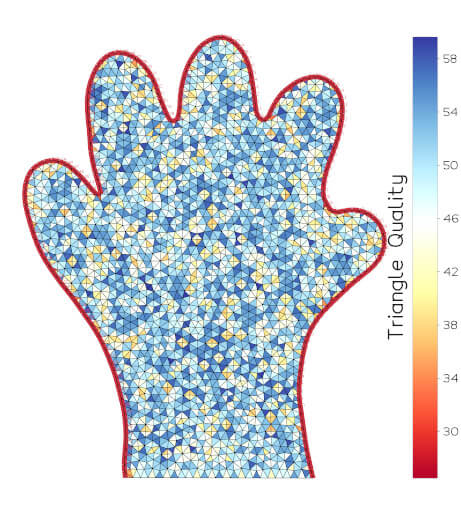               ![](https://vedo.embl.es/images/advanced/line2mesh_tri.jpg)
2823
2824            - [line2mesh_quads.py](https://github.com/marcomusy/vedo/blob/master/examples/advanced/line2mesh_quads.py)
2825
2826 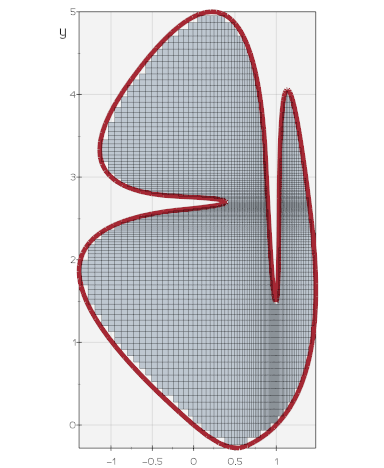               ![](https://vedo.embl.es/images/advanced/line2mesh_quads.png)
2827        """
2828        if line_resolution is None:
2829            contour = vedo.shapes.Line(self.coordinates)
2830        else:
2831            contour = vedo.shapes.Spline(self.coordinates, smooth=smooth, res=line_resolution)
2832        contour.clean()
2833
2834        length = contour.length()
2835        density = length / contour.npoints
2836        # print(f"tomesh():\n\tline length = {length}")
2837        # print(f"\tdensity = {density} length/pt_separation")
2838
2839        x0, x1 = contour.xbounds()
2840        y0, y1 = contour.ybounds()
2841
2842        if grid is None:
2843            if mesh_resolution is None:
2844                resx = int((x1 - x0) / density + 0.5)
2845                resy = int((y1 - y0) / density + 0.5)
2846                # print(f"tmesh_resolution = {[resx, resy]}")
2847            else:
2848                if utils.is_sequence(mesh_resolution):
2849                    resx, resy = mesh_resolution
2850                else:
2851                    resx, resy = mesh_resolution, mesh_resolution
2852            grid = vedo.shapes.Grid(
2853                [(x0 + x1) / 2, (y0 + y1) / 2, 0],
2854                s=((x1 - x0) * 1.025, (y1 - y0) * 1.025),
2855                res=(resx, resy),
2856            )
2857        else:
2858            grid = grid.clone()
2859
2860        cpts = contour.coordinates
2861
2862        # make sure it's closed
2863        p0, p1 = cpts[0], cpts[-1]
2864        nj = max(2, int(utils.mag(p1 - p0) / density + 0.5))
2865        joinline = vedo.shapes.Line(p1, p0, res=nj)
2866        contour = vedo.merge(contour, joinline).subsample(0.0001)
2867
2868        ####################################### quads
2869        if quads:
2870            cmesh = grid.clone().cut_with_point_loop(contour, on="cells", invert=invert)
2871            cmesh.wireframe(False).lw(0.5)
2872            cmesh.pipeline = utils.OperationNode(
2873                "generate_mesh",
2874                parents=[self, contour],
2875                comment=f"#quads {cmesh.dataset.GetNumberOfCells()}",
2876            )
2877            return cmesh
2878        #############################################
2879
2880        grid_tmp = grid.coordinates.copy()
2881
2882        if jitter:
2883            np.random.seed(0)
2884            sigma = 1.0 / np.sqrt(grid.npoints) * grid.diagonal_size() * jitter
2885            # print(f"\tsigma jittering = {sigma}")
2886            grid_tmp += np.random.rand(grid.npoints, 3) * sigma
2887            grid_tmp[:, 2] = 0.0
2888
2889        todel = []
2890        density /= np.sqrt(3)
2891        vgrid_tmp = Points(grid_tmp)
2892
2893        for p in contour.coordinates:
2894            out = vgrid_tmp.closest_point(p, radius=density, return_point_id=True)
2895            todel += out.tolist()
2896
2897        grid_tmp = grid_tmp.tolist()
2898        for index in sorted(list(set(todel)), reverse=True):
2899            del grid_tmp[index]
2900
2901        points = contour.coordinates.tolist() + grid_tmp
2902        if invert:
2903            boundary = list(reversed(range(contour.npoints)))
2904        else:
2905            boundary = list(range(contour.npoints))
2906
2907        dln = Points(points).generate_delaunay2d(mode="xy", boundaries=[boundary])
2908        dln.compute_normals(points=False)  # fixes reversd faces
2909        dln.lw(1)
2910
2911        dln.pipeline = utils.OperationNode(
2912            "generate_mesh",
2913            parents=[self, contour],
2914            comment=f"#cells {dln.dataset.GetNumberOfCells()}",
2915        )
2916        return dln
2917
2918    def reconstruct_surface(
2919        self,
2920        dims=(100, 100, 100),
2921        radius=None,
2922        sample_size=None,
2923        hole_filling=True,
2924        bounds=(),
2925        padding=0.05,
2926    ) -> "vedo.Mesh":
2927        """
2928        Surface reconstruction from a scattered cloud of points.
2929
2930        Arguments:
2931            dims : (int)
2932                number of voxels in x, y and z to control precision.
2933            radius : (float)
2934                radius of influence of each point.
2935                Smaller values generally improve performance markedly.
2936                Note that after the signed distance function is computed,
2937                any voxel taking on the value >= radius
2938                is presumed to be "unseen" or uninitialized.
2939            sample_size : (int)
2940                if normals are not present
2941                they will be calculated using this sample size per point.
2942            hole_filling : (bool)
2943                enables hole filling, this generates
2944                separating surfaces between the empty and unseen portions of the volume.
2945            bounds : (list)
2946                region in space in which to perform the sampling
2947                in format (xmin,xmax, ymin,ymax, zim, zmax)
2948            padding : (float)
2949                increase by this fraction the bounding box
2950
2951        Examples:
2952            - [recosurface.py](https://github.com/marcomusy/vedo/blob/master/examples/advanced/recosurface.py)
2953
2954                ![](https://vedo.embl.es/images/advanced/recosurface.png)
2955        """
2956        if not utils.is_sequence(dims):
2957            dims = (dims, dims, dims)
2958
2959        sdf = vtki.new("SignedDistance")
2960
2961        if len(bounds) == 6:
2962            sdf.SetBounds(bounds)
2963        else:
2964            x0, x1, y0, y1, z0, z1 = self.bounds()
2965            sdf.SetBounds(
2966                x0 - (x1 - x0) * padding,
2967                x1 + (x1 - x0) * padding,
2968                y0 - (y1 - y0) * padding,
2969                y1 + (y1 - y0) * padding,
2970                z0 - (z1 - z0) * padding,
2971                z1 + (z1 - z0) * padding,
2972            )
2973
2974        bb = sdf.GetBounds()
2975        if bb[0]==bb[1]:
2976            vedo.logger.warning("reconstruct_surface(): zero x-range")
2977        if bb[2]==bb[3]:
2978            vedo.logger.warning("reconstruct_surface(): zero y-range")
2979        if bb[4]==bb[5]:
2980            vedo.logger.warning("reconstruct_surface(): zero z-range")
2981
2982        pd = self.dataset
2983
2984        if pd.GetPointData().GetNormals():
2985            sdf.SetInputData(pd)
2986        else:
2987            normals = vtki.new("PCANormalEstimation")
2988            normals.SetInputData(pd)
2989            if not sample_size:
2990                sample_size = int(pd.GetNumberOfPoints() / 50)
2991            normals.SetSampleSize(sample_size)
2992            normals.SetNormalOrientationToGraphTraversal()
2993            sdf.SetInputConnection(normals.GetOutputPort())
2994            # print("Recalculating normals with sample size =", sample_size)
2995
2996        if radius is None:
2997            radius = self.diagonal_size() / (sum(dims) / 3) * 5
2998            # print("Calculating mesh from points with radius =", radius)
2999
3000        sdf.SetRadius(radius)
3001        sdf.SetDimensions(dims)
3002        sdf.Update()
3003
3004        surface = vtki.new("ExtractSurface")
3005        surface.SetRadius(radius * 0.99)
3006        surface.SetHoleFilling(hole_filling)
3007        surface.ComputeNormalsOff()
3008        surface.ComputeGradientsOff()
3009        surface.SetInputConnection(sdf.GetOutputPort())
3010        surface.Update()
3011        m = vedo.mesh.Mesh(surface.GetOutput(), c=self.color())
3012
3013        m.pipeline = utils.OperationNode(
3014            "reconstruct_surface",
3015            parents=[self],
3016            comment=f"#pts {m.dataset.GetNumberOfPoints()}",
3017        )
3018        return m
3019
3020    def compute_clustering(self, radius: float) -> Self:
3021        """
3022        Cluster points in space. The `radius` is the radius of local search.
3023
3024        An array named "ClusterId" is added to `pointdata`.
3025
3026        Examples:
3027            - [clustering.py](https://github.com/marcomusy/vedo/blob/master/examples/basic/clustering.py)
3028
3029                ![](https://vedo.embl.es/images/basic/clustering.png)
3030        """
3031        cluster = vtki.new("EuclideanClusterExtraction")
3032        cluster.SetInputData(self.dataset)
3033        cluster.SetExtractionModeToAllClusters()
3034        cluster.SetRadius(radius)
3035        cluster.ColorClustersOn()
3036        cluster.Update()
3037        idsarr = cluster.GetOutput().GetPointData().GetArray("ClusterId")
3038        self.dataset.GetPointData().AddArray(idsarr)
3039        self.pipeline = utils.OperationNode(
3040            "compute_clustering", parents=[self], comment=f"radius = {radius}"
3041        )
3042        return self
3043
3044    def compute_connections(self, radius, mode=0, regions=(), vrange=(0, 1), seeds=(), angle=0.0) -> Self:
3045        """
3046        Extracts and/or segments points from a point cloud based on geometric distance measures
3047        (e.g., proximity, normal alignments, etc.) and optional measures such as scalar range.
3048        The default operation is to segment the points into "connected" regions where the connection
3049        is determined by an appropriate distance measure. Each region is given a region id.
3050
3051        Optionally, the filter can output the largest connected region of points; a particular region
3052        (via id specification); those regions that are seeded using a list of input point ids;
3053        or the region of points closest to a specified position.
3054
3055        The key parameter of this filter is the radius defining a sphere around each point which defines
3056        a local neighborhood: any other points in the local neighborhood are assumed connected to the point.
3057        Note that the radius is defined in absolute terms.
3058
3059        Other parameters are used to further qualify what it means to be a neighboring point.
3060        For example, scalar range and/or point normals can be used to further constrain the neighborhood.
3061        Also the extraction mode defines how the filter operates.
3062        By default, all regions are extracted but it is possible to extract particular regions;
3063        the region closest to a seed point; seeded regions; or the largest region found while processing.
3064        By default, all regions are extracted.
3065
3066        On output, all points are labeled with a region number.
3067        However note that the number of input and output points may not be the same:
3068        if not extracting all regions then the output size may be less than the input size.
3069
3070        Arguments:
3071            radius : (float)
3072                variable specifying a local sphere used to define local point neighborhood
3073            mode : (int)
3074                - 0,  Extract all regions
3075                - 1,  Extract point seeded regions
3076                - 2,  Extract largest region
3077                - 3,  Test specified regions
3078                - 4,  Extract all regions with scalar connectivity
3079                - 5,  Extract point seeded regions
3080            regions : (list)
3081                a list of non-negative regions id to extract
3082            vrange : (list)
3083                scalar range to use to extract points based on scalar connectivity
3084            seeds : (list)
3085                a list of non-negative point seed ids
3086            angle : (list)
3087                points are connected if the angle between their normals is
3088                within this angle threshold (expressed in degrees).
3089        """
3090        # https://vtk.org/doc/nightly/html/classvtkConnectedPointsFilter.html
3091        cpf = vtki.new("ConnectedPointsFilter")
3092        cpf.SetInputData(self.dataset)
3093        cpf.SetRadius(radius)
3094        if mode == 0:  # Extract all regions
3095            pass
3096
3097        elif mode == 1:  # Extract point seeded regions
3098            cpf.SetExtractionModeToPointSeededRegions()
3099            for s in seeds:
3100                cpf.AddSeed(s)
3101
3102        elif mode == 2:  # Test largest region
3103            cpf.SetExtractionModeToLargestRegion()
3104
3105        elif mode == 3:  # Test specified regions
3106            cpf.SetExtractionModeToSpecifiedRegions()
3107            for r in regions:
3108                cpf.AddSpecifiedRegion(r)
3109
3110        elif mode == 4:  # Extract all regions with scalar connectivity
3111            cpf.SetExtractionModeToLargestRegion()
3112            cpf.ScalarConnectivityOn()
3113            cpf.SetScalarRange(vrange[0], vrange[1])
3114
3115        elif mode == 5:  # Extract point seeded regions
3116            cpf.SetExtractionModeToLargestRegion()
3117            cpf.ScalarConnectivityOn()
3118            cpf.SetScalarRange(vrange[0], vrange[1])
3119            cpf.AlignedNormalsOn()
3120            cpf.SetNormalAngle(angle)
3121
3122        cpf.Update()
3123        self._update(cpf.GetOutput(), reset_locators=False)
3124        return self
3125
3126    def compute_camera_distance(self) -> np.ndarray:
3127        """
3128        Calculate the distance from points to the camera.
3129
3130        A pointdata array is created with name 'DistanceToCamera' and returned.
3131        """
3132        if vedo.plotter_instance and vedo.plotter_instance.renderer:
3133            poly = self.dataset
3134            dc = vtki.new("DistanceToCamera")
3135            dc.SetInputData(poly)
3136            dc.SetRenderer(vedo.plotter_instance.renderer)
3137            dc.Update()
3138            self._update(dc.GetOutput(), reset_locators=False)
3139            return self.pointdata["DistanceToCamera"]
3140        return np.array([])
3141
3142    def densify(self, target_distance=0.1, nclosest=6, radius=None, niter=1, nmax=None) -> Self:
3143        """
3144        Return a copy of the cloud with new added points.
3145        The new points are created in such a way that all points in any local neighborhood are
3146        within a target distance of one another.
3147
3148        For each input point, the distance to all points in its neighborhood is computed.
3149        If any of its neighbors is further than the target distance,
3150        the edge connecting the point and its neighbor is bisected and
3151        a new point is inserted at the bisection point.
3152        A single pass is completed once all the input points are visited.
3153        Then the process repeats to the number of iterations.
3154
3155        Examples:
3156            - [densifycloud.py](https://github.com/marcomusy/vedo/blob/master/examples/volumetric/densifycloud.py)
3157
3158                ![](https://vedo.embl.es/images/volumetric/densifycloud.png)
3159
3160        .. note::
3161            Points will be created in an iterative fashion until all points in their
3162            local neighborhood are the target distance apart or less.
3163            Note that the process may terminate early due to the
3164            number of iterations. By default the target distance is set to 0.5.
3165            Note that the target_distance should be less than the radius
3166            or nothing will change on output.
3167
3168        .. warning::
3169            This class can generate a lot of points very quickly.
3170            The maximum number of iterations is by default set to =1.0 for this reason.
3171            Increase the number of iterations very carefully.
3172            Also, `nmax` can be set to limit the explosion of points.
3173            It is also recommended that a N closest neighborhood is used.
3174
3175        """
3176        src = vtki.new("ProgrammableSource")
3177        opts = self.coordinates
3178        # zeros = np.zeros(3)
3179
3180        def _read_points():
3181            output = src.GetPolyDataOutput()
3182            points = vtki.vtkPoints()
3183            for p in opts:
3184                # print(p)
3185                # if not np.array_equal(p, zeros):
3186                points.InsertNextPoint(p)
3187            output.SetPoints(points)
3188
3189        src.SetExecuteMethod(_read_points)
3190
3191        dens = vtki.new("DensifyPointCloudFilter")
3192        dens.SetInputConnection(src.GetOutputPort())
3193        # dens.SetInputData(self.dataset) # this does not work
3194        dens.InterpolateAttributeDataOn()
3195        dens.SetTargetDistance(target_distance)
3196        dens.SetMaximumNumberOfIterations(niter)
3197        if nmax:
3198            dens.SetMaximumNumberOfPoints(nmax)
3199
3200        if radius:
3201            dens.SetNeighborhoodTypeToRadius()
3202            dens.SetRadius(radius)
3203        elif nclosest:
3204            dens.SetNeighborhoodTypeToNClosest()
3205            dens.SetNumberOfClosestPoints(nclosest)
3206        else:
3207            vedo.logger.error("set either radius or nclosest")
3208            raise RuntimeError()
3209        dens.Update()
3210
3211        cld = Points(dens.GetOutput())
3212        cld.copy_properties_from(self)
3213        cld.interpolate_data_from(self, n=nclosest, radius=radius)
3214        cld.name = "DensifiedCloud"
3215        cld.pipeline = utils.OperationNode(
3216            "densify",
3217            parents=[self],
3218            c="#e9c46a:",
3219            comment=f"#pts {cld.dataset.GetNumberOfPoints()}",
3220        )
3221        return cld
3222
3223    ###############################################################################
3224    ## stuff returning a Volume
3225    ###############################################################################
3226
3227    def density(
3228        self, dims=(40, 40, 40), bounds=None, radius=None, compute_gradient=False, locator=None
3229    ) -> "vedo.Volume":
3230        """
3231        Generate a density field from a point cloud. Input can also be a set of 3D coordinates.
3232        Output is a `Volume`.
3233
3234        The local neighborhood is specified as the `radius` around each sample position (each voxel).
3235        If left to None, the radius is automatically computed as the diagonal of the bounding box
3236        and can be accessed via `vol.metadata["radius"]`.
3237        The density is expressed as the number of counts in the radius search.
3238
3239        Arguments:
3240            dims : (int, list)
3241                number of voxels in x, y and z of the output Volume.
3242            compute_gradient : (bool)
3243                Turn on/off the generation of the gradient vector,
3244                gradient magnitude scalar, and function classification scalar.
3245                By default this is off. Note that this will increase execution time
3246                and the size of the output. (The names of these point data arrays are:
3247                "Gradient", "Gradient Magnitude", and "Classification")
3248            locator : (vtkPointLocator)
3249                can be assigned from a previous call for speed (access it via `object.point_locator`).
3250
3251        Examples:
3252            - [plot_density3d.py](https://github.com/marcomusy/vedo/blob/master/examples/pyplot/plot_density3d.py)
3253
3254                ![](https://vedo.embl.es/images/pyplot/plot_density3d.png)
3255        """
3256        pdf = vtki.new("PointDensityFilter")
3257        pdf.SetInputData(self.dataset)
3258
3259        if not utils.is_sequence(dims):
3260            dims = [dims, dims, dims]
3261
3262        if bounds is None:
3263            bounds = list(self.bounds())
3264        elif len(bounds) == 4:
3265            bounds = [*bounds, 0, 0]
3266
3267        if bounds[5] - bounds[4] == 0 or len(dims) == 2:  # its 2D
3268            dims = list(dims)
3269            dims = [dims[0], dims[1], 2]
3270            diag = self.diagonal_size()
3271            bounds[5] = bounds[4] + diag / 1000
3272        pdf.SetModelBounds(bounds)
3273
3274        pdf.SetSampleDimensions(dims)
3275
3276        if locator:
3277            pdf.SetLocator(locator)
3278
3279        pdf.SetDensityEstimateToFixedRadius()
3280        if radius is None:
3281            radius = self.diagonal_size() / 20
3282        pdf.SetRadius(radius)
3283        pdf.SetComputeGradient(compute_gradient)
3284        pdf.Update()
3285
3286        vol = vedo.Volume(pdf.GetOutput()).mode(1)
3287        vol.name = "PointDensity"
3288        vol.metadata["radius"] = radius
3289        vol.locator = pdf.GetLocator()
3290        vol.pipeline = utils.OperationNode(
3291            "density", parents=[self], comment=f"dims={tuple(vol.dimensions())}"
3292        )
3293        return vol
3294
3295
3296    def tovolume(
3297        self,
3298        kernel="shepard",
3299        radius=None,
3300        n=None,
3301        bounds=None,
3302        null_value=None,
3303        dims=(25, 25, 25),
3304    ) -> "vedo.Volume":
3305        """
3306        Generate a `Volume` by interpolating a scalar
3307        or vector field which is only known on a scattered set of points or mesh.
3308        Available interpolation kernels are: shepard, gaussian, or linear.
3309
3310        Arguments:
3311            kernel : (str)
3312                interpolation kernel type [shepard]
3313            radius : (float)
3314                radius of the local search
3315            n : (int)
3316                number of point to use for interpolation
3317            bounds : (list)
3318                bounding box of the output Volume object
3319            dims : (list)
3320                dimensions of the output Volume object
3321            null_value : (float)
3322                value to be assigned to invalid points
3323
3324        Examples:
3325            - [interpolate_volume.py](https://github.com/marcomusy/vedo/blob/master/examples/volumetric/interpolate_volume.py)
3326
3327                ![](https://vedo.embl.es/images/volumetric/59095175-1ec5a300-8918-11e9-8bc0-fd35c8981e2b.jpg)
3328        """
3329        if radius is None and not n:
3330            vedo.logger.error("please set either radius or n")
3331            raise RuntimeError
3332
3333        poly = self.dataset
3334
3335        # Create a probe volume
3336        probe = vtki.vtkImageData()
3337        probe.SetDimensions(dims)
3338        if bounds is None:
3339            bounds = self.bounds()
3340        probe.SetOrigin(bounds[0], bounds[2], bounds[4])
3341        probe.SetSpacing(
3342            (bounds[1] - bounds[0]) / dims[0],
3343            (bounds[3] - bounds[2]) / dims[1],
3344            (bounds[5] - bounds[4]) / dims[2],
3345        )
3346
3347        if not self.point_locator:
3348            self.point_locator = vtki.new("PointLocator")
3349            self.point_locator.SetDataSet(poly)
3350            self.point_locator.BuildLocator()
3351
3352        if kernel == "shepard":
3353            kern = vtki.new("ShepardKernel")
3354            kern.SetPowerParameter(2)
3355        elif kernel == "gaussian":
3356            kern = vtki.new("GaussianKernel")
3357        elif kernel == "linear":
3358            kern = vtki.new("LinearKernel")
3359        else:
3360            vedo.logger.error("Error in tovolume(), available kernels are:")
3361            vedo.logger.error(" [shepard, gaussian, linear]")
3362            raise RuntimeError()
3363
3364        if radius:
3365            kern.SetRadius(radius)
3366
3367        interpolator = vtki.new("PointInterpolator")
3368        interpolator.SetInputData(probe)
3369        interpolator.SetSourceData(poly)
3370        interpolator.SetKernel(kern)
3371        interpolator.SetLocator(self.point_locator)
3372
3373        if n:
3374            kern.SetNumberOfPoints(n)
3375            kern.SetKernelFootprintToNClosest()
3376        else:
3377            kern.SetRadius(radius)
3378
3379        if null_value is not None:
3380            interpolator.SetNullValue(null_value)
3381        else:
3382            interpolator.SetNullPointsStrategyToClosestPoint()
3383        interpolator.Update()
3384
3385        vol = vedo.Volume(interpolator.GetOutput())
3386
3387        vol.pipeline = utils.OperationNode(
3388            "signed_distance",
3389            parents=[self],
3390            comment=f"dims={tuple(vol.dimensions())}",
3391            c="#e9c46a:#0096c7",
3392        )
3393        return vol
3394
3395    #################################################################################
3396    def generate_segments(self, istart=0, rmax=1e30, niter=3) -> "vedo.shapes.Lines":
3397        """
3398        Generate a line segments from a set of points.
3399        The algorithm is based on the closest point search.
3400
3401        Returns a `Line` object.
3402        This object contains the a metadata array of used vertex counts in "UsedVertexCount"
3403        and the sum of the length of the segments in "SegmentsLengthSum".
3404
3405        Arguments:
3406            istart : (int)
3407                index of the starting point
3408            rmax : (float)
3409                maximum length of a segment
3410            niter : (int)
3411                number of iterations or passes through the points
3412
3413        Examples:
3414            - [moving_least_squares1D.py](https://github.com/marcomusy/vedo/tree/master/examples/advanced/moving_least_squares1D.py)
3415        """
3416        points = self.coordinates
3417        segments = []
3418        dists = []
3419        n = len(points)
3420        used = np.zeros(n, dtype=int)
3421        for _ in range(niter):
3422            i = istart
3423            for _ in range(n):
3424                p = points[i]
3425                ids = self.closest_point(p, n=4, return_point_id=True)
3426                j = ids[1]
3427                if used[j] > 1 or [j, i] in segments:
3428                    j = ids[2]
3429                if used[j] > 1:
3430                    j = ids[3]
3431                d = np.linalg.norm(p - points[j])
3432                if used[j] > 1 or used[i] > 1 or d > rmax:
3433                    i += 1
3434                    if i >= n:
3435                        i = 0
3436                    continue
3437                used[i] += 1
3438                used[j] += 1
3439                segments.append([i, j])
3440                dists.append(d)
3441                i = j
3442        segments = np.array(segments, dtype=int)
3443
3444        lines = vedo.shapes.Lines(points[segments], c="k", lw=3)
3445        lines.metadata["UsedVertexCount"] = used
3446        lines.metadata["SegmentsLengthSum"] = np.sum(dists)
3447        lines.pipeline = utils.OperationNode("generate_segments", parents=[self])
3448        lines.name = "Segments"
3449        return lines
3450
3451    def generate_delaunay2d(
3452        self,
3453        mode="scipy",
3454        boundaries=(),
3455        tol=None,
3456        alpha=0.0,
3457        offset=0.0,
3458        transform=None,
3459    ) -> "vedo.mesh.Mesh":
3460        """
3461        Create a mesh from points in the XY plane.
3462        If `mode='fit'` then the filter computes a best fitting
3463        plane and projects the points onto it.
3464
3465        Check also `generate_mesh()`.
3466
3467        Arguments:
3468            tol : (float)
3469                specify a tolerance to control discarding of closely spaced points.
3470                This tolerance is specified as a fraction of the diagonal length of the bounding box of the points.
3471            alpha : (float)
3472                for a non-zero alpha value, only edges or triangles contained
3473                within a sphere centered at mesh vertices will be output.
3474                Otherwise, only triangles will be output.
3475            offset : (float)
3476                multiplier to control the size of the initial, bounding Delaunay triangulation.
3477            transform: (LinearTransform, NonLinearTransform)
3478                a transformation which is applied to points to generate a 2D problem.
3479                This maps a 3D dataset into a 2D dataset where triangulation can be done on the XY plane.
3480                The points are transformed and triangulated.
3481                The topology of triangulated points is used as the output topology.
3482
3483        Examples:
3484            - [delaunay2d.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/delaunay2d.py)
3485
3486                ![](https://vedo.embl.es/images/basic/delaunay2d.png)
3487        """
3488        plist = self.coordinates.copy()
3489
3490        #########################################################
3491        if mode == "scipy":
3492            from scipy.spatial import Delaunay as scipy_delaunay
3493
3494            tri = scipy_delaunay(plist[:, 0:2])
3495            return vedo.mesh.Mesh([plist, tri.simplices])
3496        ##########################################################
3497
3498        pd = vtki.vtkPolyData()
3499        vpts = vtki.vtkPoints()
3500        vpts.SetData(utils.numpy2vtk(plist, dtype=np.float32))
3501        pd.SetPoints(vpts)
3502
3503        delny = vtki.new("Delaunay2D")
3504        delny.SetInputData(pd)
3505        if tol:
3506            delny.SetTolerance(tol)
3507        delny.SetAlpha(alpha)
3508        delny.SetOffset(offset)
3509
3510        if transform:
3511            delny.SetTransform(transform.T)
3512        elif mode == "fit":
3513            delny.SetProjectionPlaneMode(vtki.get_class("VTK_BEST_FITTING_PLANE"))
3514        elif mode == "xy" and boundaries:
3515            boundary = vtki.vtkPolyData()
3516            boundary.SetPoints(vpts)
3517            cell_array = vtki.vtkCellArray()
3518            for b in boundaries:
3519                cpolygon = vtki.vtkPolygon()
3520                for idd in b:
3521                    cpolygon.GetPointIds().InsertNextId(idd)
3522                cell_array.InsertNextCell(cpolygon)
3523            boundary.SetPolys(cell_array)
3524            delny.SetSourceData(boundary)
3525
3526        delny.Update()
3527
3528        msh = vedo.mesh.Mesh(delny.GetOutput())
3529        msh.name = "Delaunay2D"
3530        msh.clean().lighting("off")
3531        msh.pipeline = utils.OperationNode(
3532            "delaunay2d",
3533            parents=[self],
3534            comment=f"#cells {msh.dataset.GetNumberOfCells()}",
3535        )
3536        return msh
3537
3538    def generate_voronoi(self, padding=0.0, fit=False, method="vtk") -> "vedo.Mesh":
3539        """
3540        Generate the 2D Voronoi convex tiling of the input points (z is ignored).
3541        The points are assumed to lie in a plane. The output is a Mesh. Each output cell is a convex polygon.
3542
3543        A cell array named "VoronoiID" is added to the output Mesh.
3544
3545        The 2D Voronoi tessellation is a tiling of space, where each Voronoi tile represents the region nearest
3546        to one of the input points. Voronoi tessellations are important in computational geometry
3547        (and many other fields), and are the dual of Delaunay triangulations.
3548
3549        Thus the triangulation is constructed in the x-y plane, and the z coordinate is ignored
3550        (although carried through to the output).
3551        If you desire to triangulate in a different plane, you can use fit=True.
3552
3553        A brief summary is as follows. Each (generating) input point is associated with
3554        an initial Voronoi tile, which is simply the bounding box of the point set.
3555        A locator is then used to identify nearby points: each neighbor in turn generates a
3556        clipping line positioned halfway between the generating point and the neighboring point,
3557        and orthogonal to the line connecting them. Clips are readily performed by evaluationg the
3558        vertices of the convex Voronoi tile as being on either side (inside,outside) of the clip line.
3559        If two intersections of the Voronoi tile are found, the portion of the tile "outside" the clip
3560        line is discarded, resulting in a new convex, Voronoi tile. As each clip occurs,
3561        the Voronoi "Flower" error metric (the union of error spheres) is compared to the extent of the region
3562        containing the neighboring clip points. The clip region (along with the points contained in it) is grown
3563        by careful expansion (e.g., outward spiraling iterator over all candidate clip points).
3564        When the Voronoi Flower is contained within the clip region, the algorithm terminates and the Voronoi
3565        tile is output. Once complete, it is possible to construct the Delaunay triangulation from the Voronoi
3566        tessellation. Note that topological and geometric information is used to generate a valid triangulation
3567        (e.g., merging points and validating topology).
3568
3569        Arguments:
3570            pts : (list)
3571                list of input points.
3572            padding : (float)
3573                padding distance. The default is 0.
3574            fit : (bool)
3575                detect automatically the best fitting plane. The default is False.
3576
3577        Examples:
3578            - [voronoi1.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/voronoi1.py)
3579
3580                ![](https://vedo.embl.es/images/basic/voronoi1.png)
3581
3582            - [voronoi2.py](https://github.com/marcomusy/vedo/tree/master/examples/basic/voronoi2.py)
3583
3584                ![](https://vedo.embl.es/images/advanced/voronoi2.png)
3585        """
3586        pts = self.coordinates
3587
3588        if method == "scipy":
3589            from scipy.spatial import Voronoi as scipy_voronoi
3590
3591            pts = np.asarray(pts)[:, (0, 1)]
3592            vor = scipy_voronoi(pts)
3593            regs = []  # filter out invalid indices
3594            for r in vor.regions:
3595                flag = True
3596                for x in r:
3597                    if x < 0:
3598                        flag = False
3599                        break
3600                if flag and len(r) > 0:
3601                    regs.append(r)
3602
3603            m = vedo.Mesh([vor.vertices, regs])
3604            m.celldata["VoronoiID"] = np.array(list(range(len(regs)))).astype(int)
3605
3606        elif method == "vtk":
3607            vor = vtki.new("Voronoi2D")
3608            if isinstance(pts, Points):
3609                vor.SetInputData(pts)
3610            else:
3611                pts = np.asarray(pts)
3612                if pts.shape[1] == 2:
3613                    pts = np.c_[pts, np.zeros(len(pts))]
3614                pd = vtki.vtkPolyData()
3615                vpts = vtki.vtkPoints()
3616                vpts.SetData(utils.numpy2vtk(pts, dtype=np.float32))
3617                pd.SetPoints(vpts)
3618                vor.SetInputData(pd)
3619            vor.SetPadding(padding)
3620            vor.SetGenerateScalarsToPointIds()
3621            if fit:
3622                vor.SetProjectionPlaneModeToBestFittingPlane()
3623            else:
3624                vor.SetProjectionPlaneModeToXYPlane()
3625            vor.Update()
3626            poly = vor.GetOutput()
3627            arr = poly.GetCellData().GetArray(0)
3628            if arr:
3629                arr.SetName("VoronoiID")
3630            m = vedo.Mesh(poly, c="orange5")
3631
3632        else:
3633            vedo.logger.error(f"Unknown method {method} in voronoi()")
3634            raise RuntimeError
3635
3636        m.lw(2).lighting("off").wireframe()
3637        m.name = "Voronoi"
3638        return m
3639
3640    ##########################################################################
3641    def generate_delaunay3d(self, radius=0, tol=None) -> "vedo.TetMesh":
3642        """
3643        Create 3D Delaunay triangulation of input points.
3644
3645        Arguments:
3646            radius : (float)
3647                specify distance (or "alpha") value to control output.
3648                For a non-zero values, only tetra contained within the circumsphere
3649                will be output.
3650            tol : (float)
3651                Specify a tolerance to control discarding of closely spaced points.
3652                This tolerance is specified as a fraction of the diagonal length of
3653                the bounding box of the points.
3654        """
3655        deln = vtki.new("Delaunay3D")
3656        deln.SetInputData(self.dataset)
3657        deln.SetAlpha(radius)
3658        deln.AlphaTetsOn()
3659        deln.AlphaTrisOff()
3660        deln.AlphaLinesOff()
3661        deln.AlphaVertsOff()
3662        deln.BoundingTriangulationOff()
3663        if tol:
3664            deln.SetTolerance(tol)
3665        deln.Update()
3666        m = vedo.TetMesh(deln.GetOutput())
3667        m.pipeline = utils.OperationNode(
3668            "generate_delaunay3d", c="#e9c46a:#edabab", parents=[self],
3669        )
3670        m.name = "Delaunay3D"
3671        return m
3672
3673    ####################################################
3674    def visible_points(self, area=(), tol=None, invert=False) -> Union[Self, None]:
3675        """
3676        Extract points based on whether they are visible or not.
3677        Visibility is determined by accessing the z-buffer of a rendering window.
3678        The position of each input point is converted into display coordinates,
3679        and then the z-value at that point is obtained.
3680        If within the user-specified tolerance, the point is considered visible.
3681        Associated data attributes are passed to the output as well.
3682
3683        This filter also allows you to specify a rectangular window in display (pixel)
3684        coordinates in which the visible points must lie.
3685
3686        Arguments:
3687            area : (list)
3688                specify a rectangular region as (xmin,xmax,ymin,ymax)
3689            tol : (float)
3690                a tolerance in normalized display coordinate system
3691            invert : (bool)
3692                select invisible points instead.
3693
3694        Example:
3695            ```python
3696            from vedo import Ellipsoid, show
3697            s = Ellipsoid().rotate_y(30)
3698
3699            # Camera options: pos, focal_point, viewup, distance
3700            camopts = dict(pos=(0,0,25), focal_point=(0,0,0))
3701            show(s, camera=camopts, offscreen=True)
3702
3703            m = s.visible_points()
3704            # print('visible pts:', m.vertices)  # numpy array
3705            show(m, new=True, axes=1).close() # optionally draw result in a new window
3706            ```
3707            ![](https://vedo.embl.es/images/feats/visible_points.png)
3708        """
3709        svp = vtki.new("SelectVisiblePoints")
3710        svp.SetInputData(self.dataset)
3711
3712        ren = None
3713        if vedo.plotter_instance:
3714            if vedo.plotter_instance.renderer:
3715                ren = vedo.plotter_instance.renderer
3716                svp.SetRenderer(ren)
3717        if not ren:
3718            vedo.logger.warning(
3719                "visible_points() can only be used after a rendering step"
3720            )
3721            return None
3722
3723        if len(area) == 2:
3724            area = utils.flatten(area)
3725        if len(area) == 4:
3726            # specify a rectangular region
3727            svp.SetSelection(area[0], area[1], area[2], area[3])
3728        if tol is not None:
3729            svp.SetTolerance(tol)
3730        if invert:
3731            svp.SelectInvisibleOn()
3732        svp.Update()
3733
3734        m = Points(svp.GetOutput())
3735        m.name = "VisiblePoints"
3736        return m